数据结构-Morris遍历

背景

对二叉树节点的遍历一般来说有中序，后序，和前序三种遍历方法，如果二叉树的高用$h$来表示，那三种遍历方法所需要的空间复杂度为$O(h)$。遍历的时候因为没有指向父节点的指针，无法从下往上走，所以采用栈，但是树的节点有很多的left，right指向null，Morris遍历利用了这些指针实现了$O(1)$的空间复杂度。

Morris遍历原理

要使用$O(1)$空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点（假设节点中没有指向父节点的p指针），由于不能用栈作为辅助空间。为了解决这个问题，Morris方法用到了线索二叉树（threaded binary tree）的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱（predecessor）和后继节点（successor），只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。

使用Morris实现中序，后序，和前序的历程都是一样的，区别在于输出打印的时机不同。记当前节点为cur。

如果当前节点无左子树，cur向右移动，cur=cur.right；
如果当前节点有左子树，找到cur左子树最右节点，记为mostRight；
1) 如果mostRight的右指针为空，则让mostRight的右指针指向cur，cur向左移动，cur=cur.left;
2) 如果mostRight的右指针指向cur，则让mostRight的右指针指向空，cur向右移动，cur=cur.right;
重复以上过程直到当前节点为空。

Morris前序顺序

当前节点的mostRight的右指针指向空，或者当前节点左子树为空格，打印该节点。具体过程为：

如果当前节点无左子树，打印当前节点，cur向右移动，cur=cur.right；
如果当前节点有左子树，找到cur左子树最右节点，记为mostRight；
1) 如果mostRight的右指针为空，则让mostRight的右指针指向cur，打印当前节点，cur向左移动，cur=cur.left;
2) 如果mostRight的右指针指向cur，则让mostRight的右指针指向空(恢复树的形状)，cur向右移动，cur=cur.right;
重复以上过程直到当前节点为空。

图示：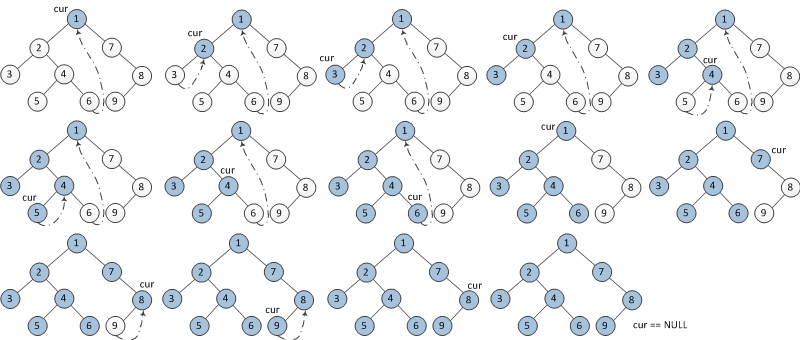
mark

代码：
leetcode 144. 二叉树的前序遍历测试通过。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """

        
        if not root:
            return []
        res = []

        cur = root
        while cur:
            if not cur.left:
                res.append(cur.val)
                cur = cur.right
            else:
                mostRight = cur.left
                while mostRight.right != None and mostRight.right != cur:
                    mostRight = mostRight.right
                if not mostRight.right:
                    res.append(cur.val)
                    mostRight.right = cur
                    cur = cur.left
                elif mostRight.right == cur:
                    mostRight.right = None
                    cur = cur.right

        return res

复杂度分析：
空间复杂度：$O(1)$，因为只用了两个辅助指针。
时间复杂度：$O(n)$。证明时间复杂度为$O(n)$，最大的疑惑在于寻找中序遍历下二叉树中所有节点的前驱节点的时间复杂度是多少，即以下两行代码：

1 2	while mostRight.right != None and mostRight.right != cur: mostRight = mostRight.right

直觉上，认为它的复杂度是$O(nlgn)$，因为找单个节点的前驱节点与树的高度有关。但事实上，寻找所有节点的前驱节点只需要$O(n)$时间。n个节点的二叉树中一共有n-1条边，整个过程中每条边最多只走2次，一次是为了定位到某个节点，另一次是为了寻找上面某个节点的前驱节点，如下图所示，其中红色是为了定位到某个节点，黑色线是为了找到前驱节点。所以复杂度为$O(n)$。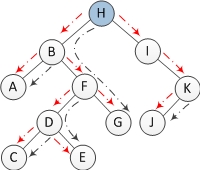
mark

Morris中序遍历

当前节点往右移动之前打印。具体过程为：

如果当前节点无左子树，打印当前节点，cur向右移动，cur=cur.right；
如果当前节点有左子树，找到cur左子树最右节点，记为mostRight；
1) 如果mostRight的右指针为空，则让mostRight的右指针指向cur，cur向左移动，cur=cur.left;
2) 如果mostRight的右指针指向cur，则让mostRight的右指针指向空，打印当前节点，cur向右移动，cur=cur.right;
重复以上过程直到当前节点为空。

图示：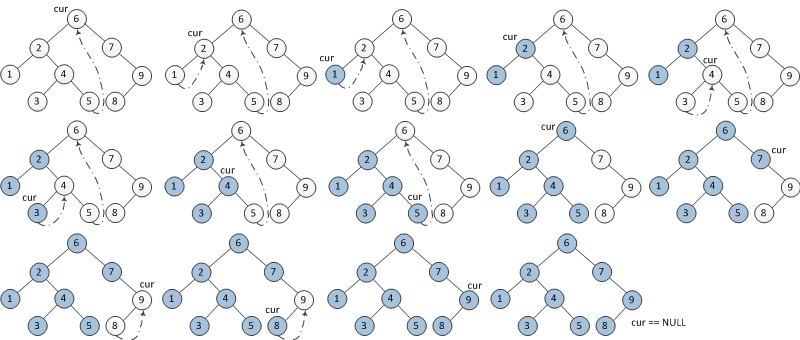
mark

代码：
leetcode 94. 二叉树的中序遍历测试通过。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        
        if not root:
            return []
        res = []

        cur = root
        while cur:
            if not cur.left:
                res.append(cur.val)
                cur = cur.right
            else:
                mostRight = cur.left
                while mostRight.right != None and mostRight.right != cur:
                    mostRight = mostRight.right
                if not mostRight.right:
                    mostRight.right = cur
                    cur = cur.left
                elif mostRight.right == cur:
                    res.append(cur.val)
                    mostRight.right = None
                    cur = cur.right

        return res

复杂度分析：
时间复杂度和空间复杂度都与前序遍历情况相同。

Morris后序遍历

当发现当前节点的mostRight的右指针指向自己，逆序打印左子树的右边界，直到当前节点为空时，逆序打印整棵树根节点的右边界。具体过程为

如果当前节点无左子树，cur向右移动，cur=cur.right；
如果当前节点有左子树，找到cur左子树最右节点，记为mostRight；
1) 如果mostRight的右指针为空，则让mostRight的右指针指向cur，cur向左移动，cur=cur.left;
2) 如果mostRight的右指针指向cur，则让mostRight的右指针指向空，逆序打印从当前节点的左子树的右边界，cur向右移动，cur=cur.right;
重复以上过程直到当前节点为空；
逆序打印整棵树根节点的右边界。

逆序打印的过程可以将该右边界上的节点看做以right指针为后继指针的链表，将其反转reverse然后打印，最后恢复成原始结构即可。

图示：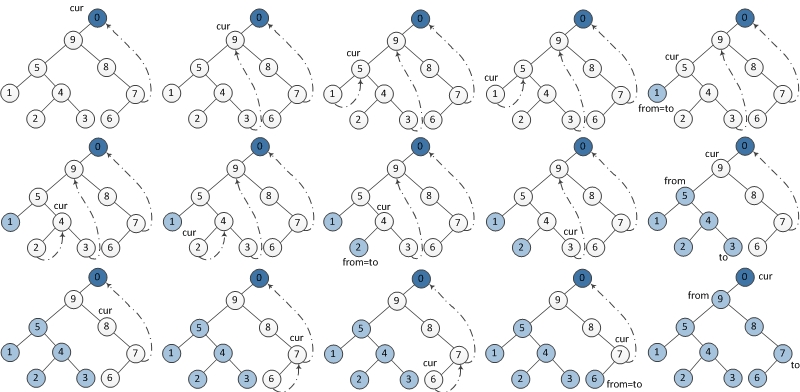
mark

代码：
leetcode 145. 二叉树的后序遍历测试通过。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def postorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        res = []

        cur = root
        while cur:
            if not cur.left:
                cur = cur.right
            else:
                mostRight = cur.left
                while mostRight.right != None and mostRight.right != cur:
                    mostRight = mostRight.right
                if not mostRight.right:
                    mostRight.right = cur
                    cur = cur.left
                elif mostRight.right == cur:
                    mostRight.right = None
                    self.printEdge(cur.left,res)
                    cur = cur.right

        self.printEdge(root, res)
        return res

    def printEdge(self, head, res):
        tail = self.reverseEdge(head)
        cur = tail
        while cur:
            res.append(cur.val)
            cur = cur.right
        self.reverseEdge(tail)

    def reverseEdge(self, head):
        pre = None
        while head:
            next = head.right
            head.right = pre
            pre = head
            head = next
        return pre