数据结构-单调栈

Posted on | Post modified: | In
Words count in article: 3.8k

单调栈的定义

单调栈就是栈内元素单调递增或者单调递减的栈，单调栈只能在栈顶操作。

为了更好的理解单调栈，则可将单调栈用生活情形模拟实现，例如：

我们借用拿号排队的场景来说明下。现在有很多人在排队买可乐，每个人手里都拿着号，越靠前的人手里的号越小，但是号不一定是连续的。小明拿了号后并没有去排队，而是跑去约会了。等他回来后，发现队伍已经排得很长了，他不能直接插入到队伍里，不然人家以为他是来插队的。小明只能跑到队伍最后，挨个询问排队人手里的号，小明认为号比他大的人都是“插队”的，于是小明就会施魔法把这些人变消失，直到小明找到号比他小的为止。

在上面这个场景里，大家排的队伍就像是单调栈，因为大家手里拿的号是单调递增的。而小明找自己位置的这个过程就是元素加入单调栈的过程。新加入的元素如果加到栈顶后，如果栈里的元素不再是单调递增了，那么我们就删除加入前的栈顶元素，就像小明施魔法把“插队”的人变消失一样。直到新元素加入后，栈依然是单调递增时，我们才把元素加进栈里。

（这样做的目的是“维护”单调栈，是单调栈保持原来的单调性不变）

单调栈的一大优势就是线性的时间复杂度$O(N)$，所有的元素只会进栈一次，而且一旦出栈后就不会再进来了。

单调递增栈可以找到左右两边最近的且比当前数字小的元素。
比如数组 [2 1 4 6 5]
刚开始2入栈，栈为[2]；
数字1入栈的时候，发现栈顶元素2比较大，将2移出栈，收集元素2左右两边最近的比2小的数，左边为null，右边为1，此后1入栈，栈为[1];
然后数字4入栈的时候，栈顶元素1小于4，4入栈，此时栈里为[1,4]
然后数字6入栈的时候，栈顶元素4小于6，6入栈，此时栈里有[1,4,6]
然后数字5入栈的时候，栈顶元素6大于5，将6移除，收集元素6左右两边最近的比6小的数，左边为4，右边为5，栈为[1,4]，此时新的栈顶元素4小于5，那么4就是5左起的第一个小的数字，收集5入栈栈内数字为 [1,4,5]。

遍历完数组之后，栈中元素出栈。
5出栈，栈为[1,4]，收集元素5左右两边最近的比5小的数，左边为4，右边为null；
4出栈，栈为[1]，收集元素4左右两边最近的比4小的数，左边为1，右边为null；
1出栈，栈为[]，收集元素1左右两边最近的比1小的数，左边为null，右边为null；

单调递减栈可以找到左右两边最近的且比当前数字大的元素。

单调栈的应用

leetcode 84. 柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。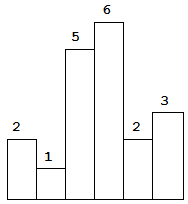
mark
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。
mark
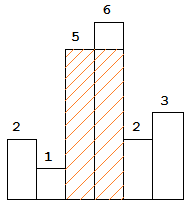
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

解题思路

使用一个递增单调栈，栈中保存坐标，数组中坐标依次入栈，当当前坐标的值小于栈顶坐标的值，则栈顶坐标弹出，并计算弹出坐标的面积，它的右边界是当前坐标的值（因为当前坐标让它出栈），左边界是栈顶坐标（当栈为空时为-1）。
当数组遍历完成后，栈不为空，则依次弹出，计算弹出坐标的面积，右边界是数组长度，左边界是栈顶坐标（当栈为空时为-1）。

例如：[2,1,5,6,2,3]
先将2的坐标入栈，栈为[0]；
元素1的坐标1入栈前比较，因为1位置的元素比栈顶(0)位置的元素小，则位置0出栈，栈为空，计算0位置的面积(1-(-1)-1)*2=2，在将1入栈，栈为[1]；
坐标2的元素5大于栈顶位置元素(1)，则坐标2入栈，栈为[1,2]；
坐标3的元素6大于栈顶位置元素(5)，则坐标3入栈，栈为[1,2,3]；
坐标4的元素2小于栈顶位置元素(6)，则将栈顶位置3弹出，栈为[1,2]，计算3位置的面积(4-2-1)*6 = 6，此时2依然小于栈顶位置2的元素5，则栈顶位置2出栈，栈为[1]，计算2位置的面积(4-1-1)*5=10；此时2大于栈顶位置元素，则2的坐标4入栈，栈为[1,4]；
坐标5的元素3大于栈顶位置元素(2)，坐标5入栈，栈为[1,4,5]；
数组遍历完成。

此时栈不为空，依次弹出计算面积。
弹出位置5，栈为[1,4]，面积为(6-4-1)*3=3;
弹出位置4，栈为[1]，面积为(6-1-1)*2=8;
弹出位置1，栈为空，面积为(6-(-1)-1)*1=6;
所以最大面积为max(2,6,10,3,8,6)=10。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """

        if len(heights) == 0:
            return 0
        res = 0
        stack = []
        for i in range(len(heights)):
            while stack and heights[i] < heights[stack[-1]]:
                index = stack.pop()
                left = stack[-1] if stack else -1
                res = max(res, (i-left-1)*heights[index])
            stack.append(i)

        while stack:
            index = stack.pop()
            left = stack[-1] if stack else -1
            res = max(res, (len(heights) - left - 1)*heights[index])

        return res

leetcode 85 最大矩形

题目描述

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

1
2
3
4
5
6
7
8
输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

解题思路

使用一个辅助数组，大小为矩阵列宽，依次以矩阵每一行为底计算最大面积，直接调用上一题的代码计算。辅助数组计算方法：初始化为0，当当前元素为1是，高度加1，为0时直接为0。
例如上例的辅助数组情况为：
第一行 [1 0 1 0 0]
第二行 [2 0 2 1 1]
第三行 [3 1 3 2 2]
第四行 [4 0 0 3 0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """

        if len(matrix) == 0:
            return 0

        heights = [0] * len(matrix[0])
        res = 0
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                heights[j] = heights[j] + 1 if matrix[i][j] == '1' else 0
            res = max(res, self.largestRectangleArea(heights))
        return res

    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """

        if len(heights) == 0:
            return 0
        res = 0
        stack = []
        for i in range(len(heights)):
            while stack and heights[i] < heights[stack[-1]]:
                index = stack.pop()
                left = stack[-1] if stack else -1
                res = max(res, (i - left - 1) * heights[index])
            stack.append(i)

        while stack:
            index = stack.pop()
            left = stack[-1] if stack else -1
            res = max(res, (len(heights) - left - 1) * heights[index])

        return res

leetcode 42. 接雨水

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
mark
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

1
2
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解题思路

解法一：先找出最高点，然后分别从左到最高点遍历，从右到最高点遍历。遍历过程中收集信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        
        if len(height) < 3:
            return 0
        
        # 求最高点处的索引
        #从左往最高点遍历
        # 从右往最高点遍历
        maxIndex = 0
        for i in range(1, len(height)):
            if height[i] > height[maxIndex]:
                maxIndex = i
        
        res = 0
        
        
        curMax = height[0]
        for i in range(1, maxIndex):
            if height[i] > curMax:
                curMax = height[i]
            else:
                res += curMax - height[i]

        curMax = height[-1]
        for i in range(len(height)-2, maxIndex, -1):
            if height[i] > curMax:
                curMax = height[i]
            else:
                res += curMax - height[i]
        
        return res

解法二：单调栈
利用一个单调递减栈，保存元素的坐标，当遇到当前高度比栈顶高度大的时候，说明有可能会有坑的存在，此时我们的栈里至少有一个高度，如果只有一个时，不能形成坑，弹出栈中元素，将当前高度压入栈，因为当前高度比栈顶高度大，替换即可。如果两个及以上时，说明形成坑了，弹出栈顶元素作为坑，右边界为当前高度，左边界为新的栈顶元素，取二者较小的减去坑的高度就为这个坑的高度，长度就是右边界坐标减去左边界左边再减1，二者相差就是这个坑的盛水量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """

        if len(height) < 3:
            return 0

        res = 0
        stack = []
        for i in range(len(height)):
            while stack and height[i] > height[stack[-1]]:
                low = stack.pop()
                if not stack:
                    break
                res += (min(height[i], height[stack[-1]]) - height[low]) * (i - stack[-1] -1)
            stack.append(i)

        return res

京东2017年笔试题 保卫方案（山峰对数量）

题目描述

战争游戏的至关重要环节就要到来了，这次的结果将决定王国的生死存亡，小B负责首都的防卫工作。首都位于一个四面环山的盆地中，周围的n个小山构成一个环，作为预警措施，小B计划在每个小山上设置一个观察哨，日夜不停的瞭望周围发生的情况。 一旦发生外地入侵事件，山顶上的岗哨将点燃烽烟，若两个岗哨所在的山峰之间没有更高的山峰遮挡且两者之间有相连通路，则岗哨可以观察到另一个山峰上的烽烟是否点燃。由于小山处于环上，任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下，一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。对于任意相邻的岗哨，一端的岗哨一定可以发现一端点燃的烽烟。 小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量，她希望你能够帮她解决这个问题。

输入描述:
输入中有多组测试数据，每一组测试数据的第一行为一个整数$n(3<=n<=10^6)$,为首都周围的小山数量，第二行为n个整数，依次表示为小山的高度$h（1<=h<=10^9）$.

输出描述:
对每组测试数据，在单独的一行中输出能相互观察到的岗哨的对数。
示例1

1
2
3
4
5
输入
5
1 2 4 5 3
输出
7

解题思路

使用单调递减的栈，栈中的数据结构是高度和该高度连续出现的次数。
找到最大值的下标，从最大值处开始循环遍历。
当遇到当前高度大于栈顶高度时，弹出栈顶元素，收集该元素的山峰对数量，等于该高度山峰内部形成的对数与该高度山峰和两边的高点形成的山峰对。
遍历完成之后，对栈中元素依次弹出，收集信息。

例如：1 2 4 5 3。
找出最大值下标，从最大值开始遍历，遍历顺序为 5 3 1 2 4。res = 0
5入栈，stack=[(5,1)]
3入栈，stack=[(5,1),(3,1)]
1入栈，stack=[(5,1),(3,1),(1,1)]
当前元素2，2大于栈顶元素1，(1,1)出栈，stack=[(5,1),(3,1)]，因为连续1只有一个，所以curTimes=1，所以连续1内部山峰对数量为curTimes*(curTimes-1)//2=0， 元素1的左边高点为当前栈顶3，右边高点为当前栈顶2，所以山峰对数量 curTimes*2=2，res = 2。
当前元素2小于当前栈顶3，2入栈，stack=[(5,1),(3,1),(2,1)]
当前元素4，4大于栈顶元素2，(2,1)出栈，stack=[(5,1),(3,1)]，因为连续2只有一个，所以curTimes=1，所以连续2内部山峰对数量为curTimes*(curTimes-1)//2=0， 元素2的左边高点为当前栈顶3，右边高点为当前栈顶4，所以山峰对数量 curTimes*2=2，res = 4。
当前元素4，4大于栈顶元素3，(3,1)出栈，stack=[(5,1)]，因为连续3只有一个，所以curTimes=1，所以连续3内部山峰对数量为curTimes*(curTimes-1)//2=0， 元素3的左边高点为当前栈顶5，右边高点为当前栈顶4，所以山峰对数量 curTimes*2=2，res = 6。
当前元素4小于当前栈顶5，4入栈，stack=[(5,1),(4,1)]

遍历完成之后，依次弹出栈中元素。
弹出(4,1)，stack=[(5,1)]，因为连续4只有一个，所以curTimes=1，所以连续4内部山峰对数量为curTimes*(curTimes-1)//2=0， 栈中元素为1个，且次数为1，4的左边高点为当前栈顶5，右边无高点，所以山峰对数量 curTimes=1，res = 7。
弹出(5,1)，stack=[]，山峰对为0。
最终山峰对为7。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

class Pair(object):
    def __init__(self, value):
        self.value = value
        self.times = 1 # 默认个数为1


class Solution(object):
    def main(self, height):

        if len(height) <= 1:
            return 0
        if len(height) == 2:
            return 1

        res = 0
        maxIndex = 0
        for i in range(1, len(height)):
            maxIndex = i if height[i] > height[maxIndex] else maxIndex

        stack = [Pair(height[maxIndex])]
        curIndex = self.nextIndex(maxIndex, len(height))
        while curIndex != maxIndex:
            while stack and height[curIndex] > stack[-1].value:
                curTimes = stack.pop().times
                # 连续相等高度内部的山峰对 + 到一个高点的山峰对
                res += curTimes*(curTimes-1)//2 + curTimes
                # 到另一个高点的山峰对
                res += curTimes if stack else 0

            if stack and stack[-1].value == height[curIndex]:
                stack[-1].times += 1
            else:
                stack.append(Pair(height[curIndex]))
            curIndex = self.nextIndex(curIndex, len(height))

        while stack:
            curTimes = stack.pop().times
            res += curTimes*(curTimes-1)//2 # 当前高度山峰内部的对数
            if stack:
                res += curTimes # 到一个高点的对数
                # 如果剩下两个以上高点的话，加上另一个高点的对数
                if len(stack) >= 2:
                    res += curTimes
                else:
                    # 如果只有一个的话，个数大于等于2，相当于有两个高点，加times
                    # 个数等于1，则只有一个高点，加0
                    res += curTimes if stack[-1].times >= 2 else 0

        return res

    def nextIndex(self, curIndex, len):
        return curIndex+1 if curIndex < len-1 else 0
    
if __name__ == '__main__':
    result = Solution().main([1,2,4,5,3])
    print(result)

参考文献
https://www.cnblogs.com/grandyang/p/8887985.html
https://blog.csdn.net/qq_35314344/article/details/76083170

Donate comment here
------------The End------------
0%