数据结构-Manacher算法

背景

给定一个字符串，求出其最长回文子串。例如：

1. s=”abcd”，最长回文长度为 1；
2. s=”ababa”，最长回文长度为 5；
3. s=”abccb”，最长回文长度为 4，即 bccb。

以上问题的传统思路大概是，遍历每一个字符，以该字符为中心向两边查找。其时间复杂度为 $O(n^2)$，效率很差。

1975 年，一个叫 Manacher 的人发明了一个算法，Manacher 算法（中文名：马拉车算法），该算法可以把时间复杂度提升到 $O(n)$。下面来看看马拉车算法是如何工作的。

算法过程

由于回文分为偶回文（比如 bccb）和奇回文（比如 bcacb），而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，具体做法是：在字符串首尾，及各字符间各插入一个字符（前提这个字符未出现在串里）。

举个例子：s="abbahopxpo"，转换为s_new="$#a#b#b#a#h#o#p#x#p#o#"（这里的字符 $ 只是为了防止越界，下面代码会有说明），如此，s 里起初有一个偶回文abba和一个奇回文opxpo，被转换为#a#b#b#a#和#o#p#x#p#o#，长度都转换成了奇数。

定义一个辅助数组int p[]，其中p[i]表示以 i 为中心的最长回文的半径，例如：

i	0	1	2	3	4	5	6	7	8	9	10	…
s[i]	#	a	#	b	#	b	#	a	#	h	#	…
p[i]	1	2	1	2	5	2	1	2	1	2	1	…

可以看出，p[i] - 1正好是原字符串中最长回文串的长度。

接下来的重点就是求解 p 数组，如下图：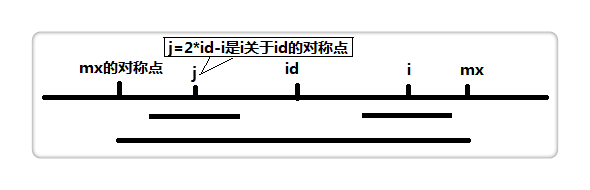

设置两个变量，mx 和 id 。mx 代表以 id 为中心的最长回文的右边界，也就是mx = id + p[id]。

假设我们现在求p[i]，也就是以 i 为中心的最长回文半径，如果i < mx，如上图，那么：

if (i < mx)  
    p[i] = min(p[2 * id - i], mx - i);

2 * id - i为 i 关于 id 的对称点，即上图的 j 点，而p[j]表示以 j 为中心的最长回文半径，因此我们可以利用p[j]来加快查找。

代码

class Solution(object):
    def manacher(self, s):
        if len(s) == 0:
            return 0

        s = self.init(s)
        p = [0] * len(s)
        id = -1
        mx = -1
        res = 0
        center = 0
        for i in range(len(s)):
            p[i] = min(p[2*id-i], mx-i) if i < mx else 1
            while i + p[i] < len(s) and i - p[i] > -1:
                if s[i+p[i]] == s[i-p[i]]:
                    p[i] += 1
                else:
                    break
            if i + p[i] > mx:
                mx = i + p[i]
                id = i # id是最右回文子串的中心

        return res-1

    def init(self, s):

        res = '#'
        for i in range(len(s)):
            res += s[i]
            res += '#'
        return res


if __name__ == '__main__':
    res = Solution().manacher("cbbd")
    print(res)
`

算法复杂度分析

文章开头已经提及，Manacher 算法为线性算法，即使最差情况下其时间复杂度亦为 O(n)O(n)，在进行证明之前，我们还需要更加深入地理解上述算法过程。

根据回文的性质，p[i]的值基于以下三种情况得出：

（1）：j 的回文串有一部分在 id 的之外，如下图：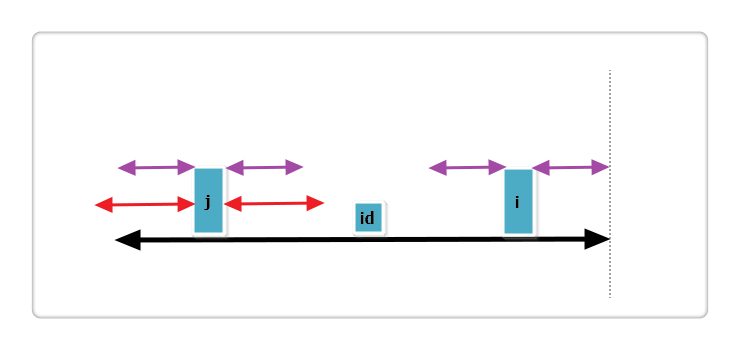

上图中，黑线为 id 的回文，i 与 j 关于 id 对称，红线为 j 的回文。那么根据代码此时p[i] = mx - i，即紫线。那么p[i]还可以更大么？答案是不可能！见下图：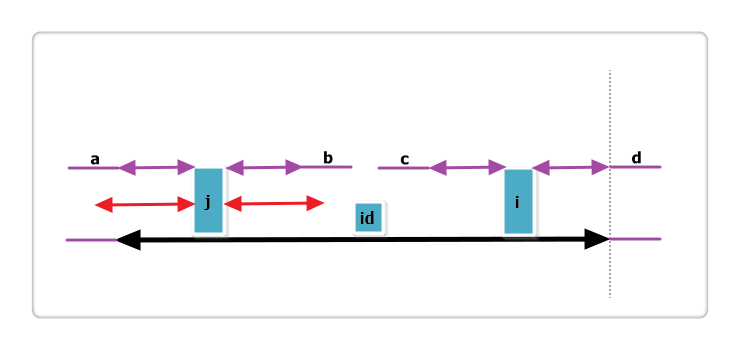

假设右侧新增的紫色部分是p[i]可以增加的部分，那么根据回文的性质，a 等于 d ，也就是说 id 的回文不仅仅是黑线，而是黑线 + 两条紫线，矛盾，所以假设不成立，故p[i] = mx - i，不可以再增加一分。

（2）：j 回文串全部在 id 的内部，如下图：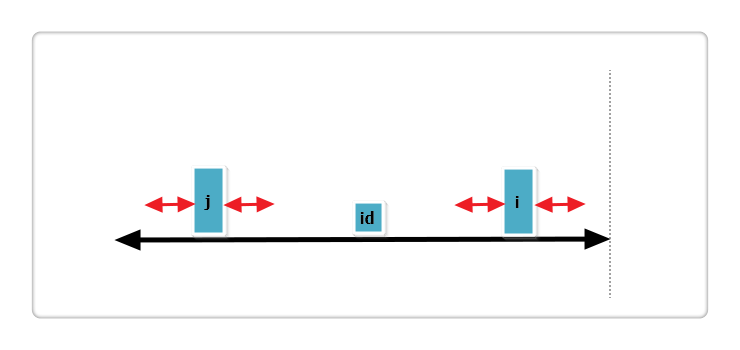

根据代码，此时p[i] = p[j]，那么p[i]还可以更大么？答案亦是不可能！见下图：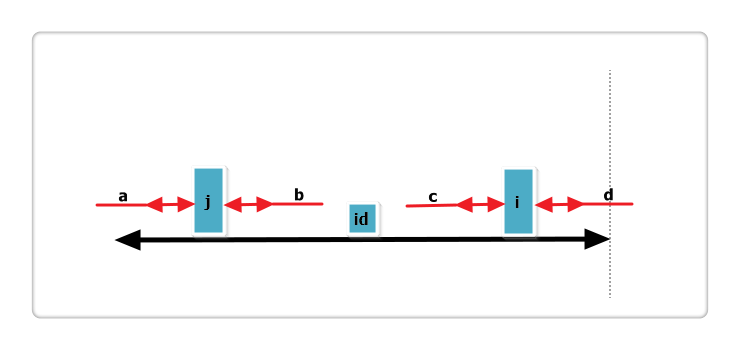

假设右侧新增的红色部分是p[i]可以增加的部分，那么根据回文的性质，a 等于 b ，也就是说 j 的回文应该再加上 a 和 b ，矛盾，所以假设不成立，故p[i] = p[j]，也不可以再增加一分。

（3）：j 回文串左端正好与 id 的回文串左端重合，见下图：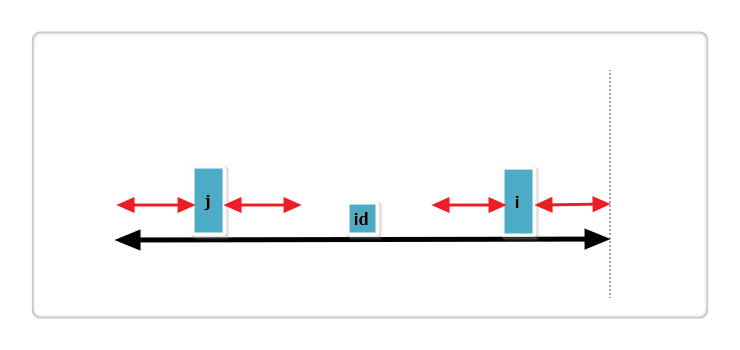

根据代码，此时p[i] = p[j]或p[i] = mx - i，并且p[i]还可以继续增加，所以需要

while (s[i - p[i]] == s[i + p[i]]) 
    p[i]++;

根据（1）（2）（3），很容易推出 Manacher 算法的最坏情况，即为字符串内全是相同字符的时候。在这里我们重点研究 Manacher（）中的 for 语句，推算发现 for 语句内平均访问每个字符 5 次，即时间复杂度为：$T_{worst}(n)=O(n)$。

同理，我们也很容易知道最佳情况下的时间复杂度，即字符串内字符各不相同的时候。推算得平均访问每个字符 4 次，即时间复杂度为：$T_{best}(n)=O(n)$。

综上，Manacher 算法的时间复杂度为 $O(n)$。

例子：

leetcode 5. 最长回文子串

题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。

示例 2：

输入: “cbbd”
输出: “bb”

解题思路

暴力解决

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) < 2:
            return s
        maxlen = 0
        start = 0
        for i in range(len(s)):
            for j in range(i+1, len(s)+1):
                if s[i:j] == s[i:j][::-1] and j-i > maxlen:
                    maxlen = j-i
                    start = i
        if maxlen > 0:
            return s[start:start+maxlen]
        return ''

动态规划

动态规划有两个特点：将大问题拆解为小问题，利用之前的计算结果。

例子：”babad”
新建dp二维数组,
$dp[i][j]=1$
时则说明第i到第j为回文子串。

[[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0]]

• 首先计算长度为1的子串，必定是回文；
• 然后判断长度为2的子串，根据相等与否判断是否为回文；
• 到长度为3时，就可以利用上次的计算结果：
  • 如果中心对称的短字符串(去掉头尾，此时只有第2个位置的一个字符)是回文，且如果第1和第3个位置相等，则长字符串也是回文；如果第1和第3个位置不相等，则长字符串不是回文；
  • 如果中心对称的短字符串(去掉头尾)不是回文，则长字符串也不是回文；
• 一直遍历到长度最长的字符串。

即当i=j+1时相邻是为长度为2的情况，当i-j > 2时为长度为3的情况，递推式为：
$dp[i][i] = 1$
$dp[j][i] = (s[i] == s[j]) \& (i-j<=2 | dp[j + 1][i - 1])$

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) < 2:
            return s
        dp = [[0]*len(s) for _ in range(len(s))]
        start, end, maxlen = 0, 0, 0
        for i in range(len(s)):
            for j in range(i):
                dp[j][i] = (s[i]==s[j]) & ((i-j<=2) | dp[j+1][i-1])
                if dp[j][i] and maxlen < i-j+1:
                    maxlen = i-j+1
                    start = j
                    end = i
            dp[i][i] = 1
        return s[start:end+1]

Manacher算法

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        
        if len(s) == 0:
            return ''

        s = self.init(s)
        p = [0] * len(s)
        id = -1 # 记录最右回文子串的中心
        mx = -1
        res = 0
        maxCenter = 0 # 记录最长回文子串的中心
        for i in range(len(s)):
            p[i] = min(p[2*id-i], mx-i) if i < mx else 1
            while i + p[i] < len(s) and i - p[i] > -1:
                if s[i+p[i]] == s[i-p[i]]:
                    p[i] += 1
                else:
                    break
            if i + p[i] > mx:
                mx = i + p[i]
                id = i
            if p[i] > res:
                maxCenter = i
                res = p[i]

        return ''.join(s[maxCenter-(res-1):maxCenter+res-1+1].split('#'))

    def init(self, s):

        res = '#'
        for i in range(len(s)):
            res += s[i]
            res += '#'
        return res
`

在字符串后面添加最少字符使成为回文字符串

解题思路

使用马拉车算法求解，求得最右回文子串，其左边的逆序添加到后面即整体变为回文。添加的长度为最右回文子串的左边部分长度。

class Solution(object):
    def manacher(self, s):
        if len(s) == 0:
            return 0

        new_s = self.init(s)
        p = [0] * len(new_s)
        id = -1
        mx = -1
        maxContainsEnd = -1
        for i in range(len(new_s)):
            p[i] = min(p[2*id-i], mx-i) if i < mx else 1
            while i + p[i] < len(new_s) and i - p[i] > -1:
                if new_s[i+p[i]] == new_s[i-p[i]]:
                    p[i] += 1
                else:
                    break
            if i + p[i] > mx:
                mx = i + p[i]
                id = i
            if  mx == len(new_s):
                maxContainsEnd = p[i]
                break

        return len(s) - (maxContainsEnd -1)

    def init(self, s):

        res = '#'
        for i in range(len(s)):
            res += s[i]
            res += '#'
        return res


if __name__ == '__main__':
    res = Solution().manacher("abcd123321")
    print(res)

Reference：https://subetter.com/algorithm/manacher-algorithm.html