数据结构-并查集

Posted on | Post modified: | In
Words count in article: 2.3k

本系列为数据结构学习笔记(待汇总)。

合并-查找问题

什么是合并查找问题呢？顾名思义，就是既有合并又有查找操作的问题。举个例子，有一群人，他们之间有若干好友关系。如果两个人有直接或者间接好友关系，那么我们就说他们在同一个朋友圈中，这里解释下，如果Alice是Bob好友的好友，或者好友的好友的好友等等，即通过若干好友可以认识，那么我们说Alice和Bob是间接好友。随着时间的变化，这群人中有可能会有新的朋友关系，这时候我们会对当中某些人是否在同一朋友圈进行询问。这就是一个典型的合并－查找操作问题，既包含了合并操作，又包含了查找操作。

这个问题很容易想到朴素算法，每个人用一个编号来表示他所在的朋友圈，如果有新认识的朋友，我们就合并朋友圈，即把两人的朋友圈中所有人编号标识成一样。

mark

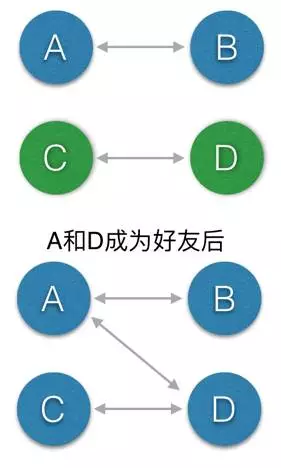
简单解释一下这个图，刚开始A和B是好友，用蓝色背景标记，C和D是好友，用绿色背景标记，如果询问两个人是否在同一个朋友圈，那么只要看一下他们标记是否相同。过了不久，A和D又成为了好友，我们把两个朋友圈中所有的人标记变成相同的颜色，这就完成了一次合并的操作。

我们来粗略的计算下复杂度，假设我们要合并Alice和Bob的朋友圈，需要找到所有和Bob在同一朋友圈里的人，并标记为Alice所在的朋友圈。代码如下

1
2
3
4
5
# group[i]表示i所在的朋友圈编号
# 将朋友圈B合并到朋友圈A中
for i in range(n):
	if group[i] == group[B]:
		group[i] = group[A]

合并代码非常简单，那么可以看到一次合并的复杂度为$O(n)$，一共有n个人，因此最多可能要合并$n-1$次，合并的复杂度为$n^2$，加上Q个朋友圈询问，那么总的复杂度就是$O(n^2+Q)$。当n很大的时候，算法是不可接受的。

并查集

这个时候我们就希望重新设计一种数据结构，能够高效的处理这三种操作，分别是

  • MAKE-SET(x)，创建一个只有元素x的集合，且x不应出现在其他的集合中

  • UNION(x, y)，将元素x所在集合Sx和元素y所在的集合Sy合并，这里我们假定Sx不等于Sy

  • FIND-SET(x)，查找元素x所在集合的代表

现在我们再来看一下刚刚那道题，起初每个人都互相不认识，我们可以调用n次MAKE-SET来创建n个集合，当有两个人互相认识的时候，那么我们用UNION来合并两个集合。最后，如果询问x和y是否在同一个朋友圈的时候，我们调用两次FIND-SET来判断x和y所在集合的代表是否相同，从而判断他们是否在同一个集合内。

这个时候就该并查集出场了，它能够高效的处理前面提到的三种操作，用于维护一系列不相交集合动态操作的数据结构。每个不相交集合都有一个代表用于表示整个集合，并且这个代表也是集合内的成员。下面来说一下并查集是如何工作的。在并查集中，每个不相交的集合都用一颗有根树来表示，每个元素都是树上的一个节点，我们继续用刚刚的朋友圈问题来解释。

mark

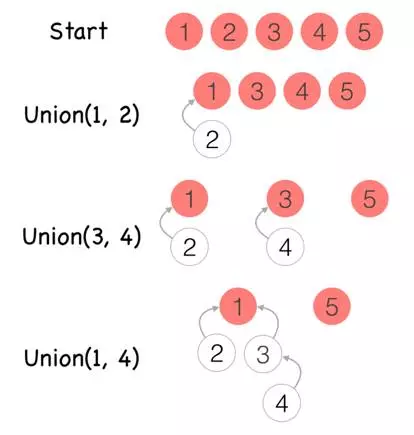
我们来解释下这个图，起初有5个人，编号为1-5，刚开始大家都互不认识，所以各自为一个节点的树。这时候如果1和2认识了，那么我们就把这两个节点所代表的树合并起来，由编号较小的1作为根。接着3和4又认识了，那么我们重复刚刚的过程，把3和4所代表树合并起来。现在1和4认识了，该怎么办呢，首先我们先找到1和4所在树的根，1的根就是1，而4的根就是3，这时候我们把这两颗树合并，并把1设置为3的父亲节点，这时候就完成了两颗树的合并。在这系列操作中，初始化构建树就是MAKE-SET操作，树的合并就是UNION操作，而找根的过程就是FIND-SET操作。

下面讲一讲并查集的具体实现。对于有根树或者说森林的表示，可以用一个数组parent来实现。parent[i]记录元素i的父节点的编号，如果节点i本身就是根节点，那么parent[i]就是-1。MAKE-SET操作就是将parent数组赋值为-1。

1
2
3
def MAKE_SET(self, arr):
	parent = [-1]*len(arr)
	return parent

UNION操作需要找到两个元素的根，并把其中一个元素的根节点设置为另一个元素的根节点，其实就是调用了两次FIND-SET，代码如下

1
2
3
4
5
6
7
8
# 将y所在的集合合并到x所在的集合中
# 分别查找出x和y所在集合的根节点
# 将y元素所在的集合的代表节点的根节点设置为x所在集合的根节点
def union(self, x, y):
	px = find_set(x)
	py = find_set(y)
	if px != py:
		parent[py] = px

再来说下FIND-SET这个操作的实现。首先有个很朴素的算法，对父节点递归调用FIND-SET，直到找到根为止。如果父节点是-1，那么返回当前节点，否则递归调用查询父亲的根节点。代码如下

1
2
3
4
5
# 递归查找x所在集合的根节点
def find_set(self, x):
	if parent[x] == -1:
		return x
	return find_set(parent[x])

但是，如果我们这棵树很深，那么每次调用FIND-SET可能会需要O(n)的时间。

这时候，我们就要引入路径压缩这个概念。什么是路径压缩呢？就是在递归找到根节点的时候，把当前节点到根节点间所有节点的父节点都设置为根节点。举个例子

mark

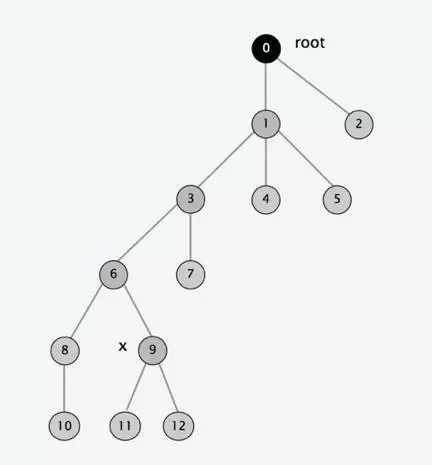
我们来看下图，首先我们有个这样的一棵树，现在要找到元素9所在树的根节点，在找根节点的过程中使用路径压缩，也就是说9到根的路径上的节点9，6，3，1的父节点都设置成为根节点0，所以呢，在FIND-SET(9)之后，树的形态就变成了下面的样子

mark

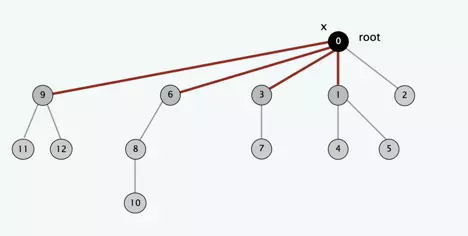
我们可以看到经过路径压缩的节点及其子树到根节点的深度减小了很多，所以在以后的操作中，查找根节点的速度会快很多，平摊下来每次FIND-SET的操作几乎是常数级别的。代码也相当简单，就只多了一句话

1
2
3
4
5
6
# 带有路径压缩的并查集
def find_set(self, x):
	if parent[x] == -1:
		return x
	parent[x] = find_set(parent[x])
	return parent[x]

刚刚在合并的过程中，并没有提到说到如何选取根，一般情况下两个根节点随意选取一个，如果需要更优的算法，可以按秩合并，就是在合并之前，先判断下哪棵子树更高，让矮的子树的根指向高的子树的根。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 初始化根节点为-1
# 初始化各集合大小为1
def MAKE_SET(self, arr):
	parent = [-1] * len(arr)
	sizeMap = [1] * len(arr)
	return parent

def union(self, x, y):
	px = find_set(x)
	py = find_set(y)
	if px != py:
		xSize = sizeMap[px]
		ySize = sizeMap[py]
		if xSize <= ySize:
			parent[px] = py
			sizeMap[py] = xSize + ySize
		else:
			parent[py] = px
			sizeMap[px] = xSize + ySize

并查集是一种支持合并集合和查找集合的一种数据结构，能用均摊线性的复杂度执行各种操作，在kruskal算法、求联通分支数等算法中起到关键的作用。

总结

为了表示一个元素所属的集合，我们从一个集合当中挑选出一个代表元素作为根节点。对于每个元素，都记录一下它对应的根节点是谁，这样就可以通过根节点来表示它所述的集合。在集合合并时，如果对一个小集合中的所有元素都修改其根节点，则会造成合并的开销过大。为了减小开销，我们在合并时采取层次化的结构，按照按秩合并的方法，可以使合并操作的复杂度降为O(1)，但是这在减少合并开销的同时又增加了查询开销，使得总开销并没有降低。为了进一步减少查询开销，引入了路径压缩这个操作，使得长路径上的检索只需要发生一次。

参考文献：
https://mp.weixin.qq.com/s/50QN956P6Udpo4AKlWfeew
https://zhuanlan.zhihu.com/p/54567565
https://zhuanlan.zhihu.com/p/54727138

Donate comment here
------------The End------------
0%