数据结构-字典树

Posted on | Post modified: | In
Words count in article: 2k

本系列为数据结构学习笔记(待汇总)。

字典树

字典树，即Trie树，又称单词查找树或键树，是一种树形结构，常用于统计和排序大量字符串等场景（但不限于字符串），且经常被搜索引擎用于文本词频统计。它的优点是最大限度减少无谓的字符串比较，查询效率比较高。
Trie树的核心思想是以空间换时间，利用字符串的公共前缀来降低查询时间的开销，以达到提高效率的目的。
它有以下三个基本性质：

  • 根结点不包含字符，除根结点外每一个结点都只包含一个字符；
  • 从根节点到某一节点。路径上经过的字符连接起来，就是该节点对应的字符串；
  • 每个节点的所有子节点包含的字符都不相同。

树的构建

举例：
题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。
分析：这题当然可以用hash来解决，但是本文重点介绍的是trie树，因为在某些方面它的用途更大。比如说对于某一个单词，我们要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单。
现在回到例子中，如果我们用最傻的方法，对于每一个单词，我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是$O(n^2)$。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd，那么在他前面的单词中，以b，c，d，f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的，在以a开头中的单词中，我们只要考虑以b作为第二个字母的，一次次缩小范围和提高针对性，这样一个树的模型就渐渐清晰了。
好比假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词，我们构建的树就是如下图这样的：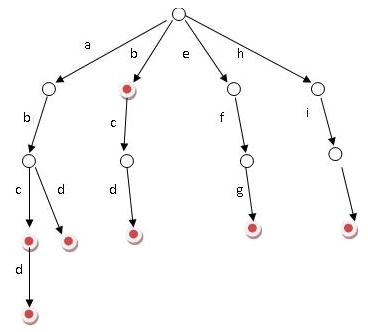
mark

如上图所示，从根结点遍历到每个结点的路径就是一个单词，如果这个结点被标记为红色，就表示这个单词存在，否则不存在。
那么，对于一个单词，只要顺着它从根走到对应的结点，再看这个结点是否被标记为红色就可以知道它是否出现过了。
把这个节点标记为红色，就相当于插入了这个单词。这样一来我们查询和插入可以一起完成
我们可以看到，trie树每一层的节点数是$26^i$级别的。为了节省空间，还可以动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数乘以单词长度。

查询

Trie树是简单但实用的数据结构，通常用于实现字典查询。我们做即时响应用户输入的AJAX搜索框时，就是Trie开始。本质上，Trie是一颗存储多个字符串的树。相邻节点间的边代表一个字符，这样树的每条分支代表一则子串，而树的叶节点则代表完整的字符串。和普通树不同的地方是，相同的字符串前缀共享同一条分支。下面，再举一个例子。给出一组单词，inn, int, at, age, adv, ant, 我们可以得到下面的Trie：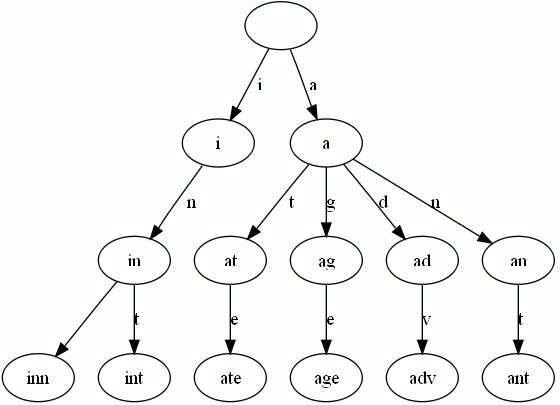
mark

可以看出：

  • 每条边对应一个字母。
  • 每个节点对应一项前缀。叶节点对应最长前缀，即单词本身。
  • 单词inn与单词int有共同的前缀“in”, 因此他们共享左边的一条分支，root->i->in。同理，ate, age, adv, 和ant共享前缀”a”，所以他们共享从根节点到节点”a”的边。

查询操纵非常简单。比如要查找int，顺着路径i -> in -> int就找到了。

搭建Trie的基本算法也很简单，无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在，就共享，否则创建对应的节点和边。比如要插入单词add，就有下面几步：
考察前缀”a”，发现边a已经存在。于是顺着边a走到节点a。
考察剩下的字符串”dd”的前缀”d”，发现从节点a出发，已经有边d存在。于是顺着边d走到节点ad
考察最后一个字符”d”，这下从节点ad出发没有边d了，于是创建节点ad的子节点add，并把边ad->add标记为d。

实现

性质：

  • 根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
  • 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
  • 每个节点的所有子节点包含的字符互不相同。
  • 通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

可以看出，Trie树的关键字一般都是字符串，而且Trie树把每个关键字保存在一条路径上，而不是一个结点中。另外，两个有公共前缀的关键字，在Trie树中前缀部分的路径相同，所以Trie树又叫做前缀树（Prefix Tree）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import collections
class Node(object):
    def __init__(self):
        self.children = collections.defaultdict(Node)
        self.isWord = False

class Trie(object):

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.root = Node()

    def insert(self, word):
        """
        Inserts a word into the trie.
        :type word: str
        :rtype: None
        """
        cur = self.root
        for w in word:
            cur = cur.children[w]
        cur.isWord = True

    def search(self, word):
        """
        Returns if the word is in the trie.
        :type word: str
        :rtype: bool
        """
        cur = self.root
        for w in word:
            cur = cur.children.get(w)
            if not cur:
                return False
        return cur.isWord

    def startsWith(self, prefix):
        """
        Returns if there is any word in the trie that starts with the given prefix.
        :type prefix: str
        :rtype: bool
        """
        cur = self.root
        for w in prefix:
            cur = cur.children.get(w)
            if not cur:
                return False
        return True



if __name__ == '__main__':
# Your Trie object will be instantiated and called as such:
    obj = Trie()
    obj.insert('apple')
    print(obj.search('apple'))
    print(obj.search('app'))
    print(obj.startsWith('app'))
    obj.insert('app')
    print(obj.search('app'))

问题实例

  • Q. 10个频繁出现的词： 一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。
    A. 用Trie树统计每个词出现的次数，时间复杂度是$O(nl)$（$l$表示单词的平均长度，最终用最小堆找到出现次数最频繁的10个词，时间复杂度为$O(nlog10)$

  • 寻找热门查询：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有1000万个记录，这些查询串的重复度比较高，虽然总数是1000万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。
    A. 可以使用Trie树，观察关键字在该查询串出现的次数，若没有出现则为0，最后用10个元素的最小堆来对出现频率进行排序。

参考文献：
从Trie树（字典树）谈到后缀树

Donate comment here
------------The End------------
0%