本系列为Leetcode刷题笔记，刷题平台为Leetcode中文站，刷题按Tag分类。本系列题解汇总如下 (持续更新…)：

本文主要是搜索相关题目题解总结。

[TOC]

搜索

本文内容主要包括广度优先搜索(breadth first search)，深度优先搜索(depth first search)。

广度优先搜索(BFS)

主要思想：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点依次访问它们的邻接点，并使得先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起点，重复上述过程，直至图中所有顶点都被访问到。

注意：遍历过的节点不能再次被遍历。

每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离，推导出一个结论：
对于先遍历的节点 i 与后遍历的节点 j，有 di <= dj。利用这个结论，可以求解最短路径等 最优解 问题：第一次遍历到目的节点，其所经过的路径为最短路径。应该注意的是，使用 BFS 只能求解无权图的最短路径。

实现 BFS 时需要考虑以下问题：
队列：用来存储每一轮遍历得到的节点；
标记：对于遍历过的节点，应该将它标记，防止重复遍历。

无向图的广度优先搜索

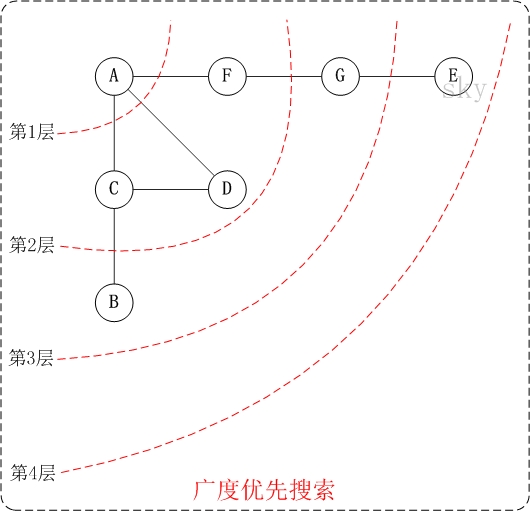
第1步：访问A。并将C，D，F加入到访问队列，[C,D,F]
第2步：访问C。并将 B加入到访问队列，[D,F,B]
第3步：访问D。由于D的邻接点C已经访问过，则不加入访问队列，[F,B];
第4步：访问F。并将G加入访问队列，[B,G];
第5步：访问B。
第6步：访问G。并将E加入到访问队列，[E];
第7步：访问E。
因此访问顺序是：A -> C -> D -> F -> B -> G -> E
有向图的广度优先搜索
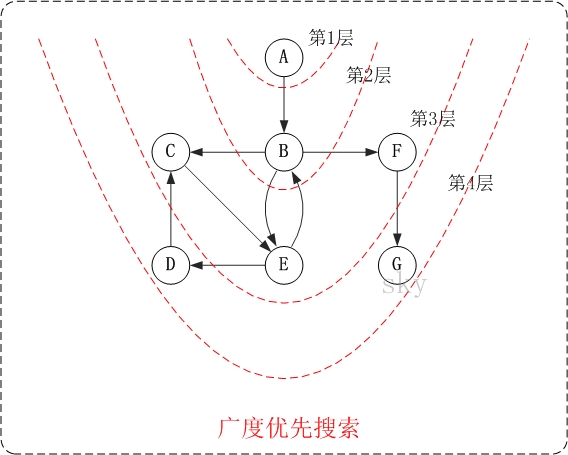
访问顺序：A -> B -> C -> E -> F -> D -> G

深度优先搜索(DFS)

主要思想：假设初始状态所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历，直到所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作为起始点，重复上述过程，直到所有顶点都被访问到。

深度优先搜索是一个递归的过程。

从一个节点出发，使用 DFS 对一个图进行遍历时，能够遍历到的节点都是从初始节点可达的，DFS 常用来求解这种可达性问题。

实现 DFS 时需要考虑以下问题：
栈：用栈来保存当前节点信息，当遍历新节点返回时能够继续遍历当前节点。可以使用递归栈。
标记：和 BFS 一样同样需要对已经遍历过的节点进行标记。

无向图的深度优先搜索

访问顺序是：A -> C -> B -> D -> F -> G -> E

有向图的深度优先搜索

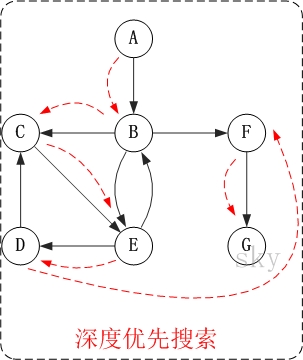
访问顺序是：A -> B -> C -> E -> D -> F -> G

参考

127. 单词接龙

题目描述

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。

说明:

如果不存在这样的转换序列，返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的，且二者不相同。
示例 1:

输入:
beginWord = “hit”,
endWord = “cog”,
wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
输出: 5
解释: 一个最短转换序列是 “hit” -“hot” -“dot” -“dog” -“cog”, 返回它的长度 5。
示例 2:

输入:
beginWord = “hit”
endWord = “cog”
wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
输出: 0
解释: endWord “cog” 不在字典中，所以无法进行转换。

解题思路

使用BFS，最短路的思路。将beginWord放进队列，如果队列不为空，那么取出第一个数，将其周围的在字典的字符放进队列，直到周围的存在endword。

import collections
class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordList = set(wordList)
        queue = collections.deque()
        queue.append([beginWord, 1])
        while queue:
            word, length = queue.popleft()
            if word == endWord:
                return length
            for i in range(len(word)):
                for c in 'abcdefghijklmnopqrstuvwxyz':
                    nextWord = word[:i] + c + word[i + 1:]
                    if nextWord in wordList:
                        wordList.remove(nextWord)
                        queue.append([nextWord, length + 1])
        return 0
if __name__ == '__main__':
    result = Solution().ladderLength("hit","cog",["hot","dot","dog","lot","log","cog"])
    print(result)

class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordList = set(wordList)
        stack = [(beginWord, 1)]

        while stack:
            word, length = stack.pop(0)
            if word == endWord:
                return length

            for i in range(len(word)):
                for c in 'abcdefghijklmnopqrstuvwxyz':
                    nextWord = word[:i] + c + word[i+1:]
                    if nextWord in wordList:
                        wordList.remove(nextWord)
                        stack.append((nextWord, length+1))

        return 0

130. 被围绕的区域

题目描述

给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O）。

找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

示例:

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

解题思路

从边上开始搜索，如果是’O’,那么搜索’O’周围的元素，并将’O’置换为’D’。如果该’O’周围都是’X’，则会跳出，这样内部的’O’将不受影响。最后没有被’X’围住的’O’都置换成了’D’,被围住的’O’还是’O’，没有改变。然后遍历一遍，将’O’置换为’X’，将’D’置换为’O’。

在Leetcode中文网站无法提交，英文网站正常。

迭代 BFS。

class Solution(object):
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: void Do not return anything, modify board in-place instead.
        """
        import collections
        queue = collections.deque([])
        for r in range(len(board)):
            for c in range(len(board[0])):
                if (r in [0, len(board) - 1] or c in [0, len(board[0]) - 1]) and board[r][c] == "O":
                    queue.append((r, c))
        while queue:
            r, c = queue.popleft()
            if 0 <= r < len(board) and 0 <= c < len(board[0]) and board[r][c] == "O":
                board[r][c] = "D"
                queue.append((r - 1, c))
                queue.append((r + 1, c))
                queue.append((r, c - 1))
                queue.append((r, c + 1))

        for r in range(len(board)):
            for c in range(len(board[0])):
                if board[r][c] == "O":
                    board[r][c] = "X"
                elif board[r][c] == "D":
                    board[r][c] = "O"

递归 DFS

class Solution(object):
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: void Do not return anything, modify board in-place instead.
        """
        for r in range(len(board)):
            for c in range(len(board[0])):
                if (r in [0, len(board)-1] or c in [0, len(board[0])-1]) and board[r][c] == 'O':
                    self.dfs(board, r, c)
        for r in range(len(board)):
            for c in range(len(board[0])):
                if board[r][c] == 'O':
                    board[r][c] = 'X'
                elif board[r][c] == 'D':
                    board[r][c] = 'O'
    def dfs(self, board, r, c):
        if 0 <= r < len(board) and 0 <= c < len(board[0]) and board[r][c] == 'O':
            board[r][c] = 'D'
            self.dfs(board, r-1, c)
            self.dfs(board, r+1, c)
            self.dfs(board, r, c-1)
            self.dfs(board, r, c+1)

133. 克隆图

题目描述

克隆一张无向图，图中的每个节点包含一个 label （标签）和一个 neighbors （邻接点）列表。

OJ的无向图序列化：

节点被唯一标记。

我们用 # 作为每个节点的分隔符，用 , 作为节点标签和邻接点的分隔符。

例如，序列化无向图 {0,1,2#1,2#2,2}。

该图总共有三个节点, 被两个分隔符 # 分为三部分。

第一个节点的标签为 0，存在从节点 0 到节点 1 和节点 2 的两条边。
第二个节点的标签为 1，存在从节点 1 到节点 2 的一条边。
第三个节点的标签为 2，存在从节点 2 到节点 2 (本身) 的一条边，从而形成自环。

我们将图形可视化如下：

解题思路

由于遍历一个图有两种方式：bfs和dfs。所以深拷贝一个图也可以采用这两种方法。不管使用dfs还是bfs都需要一个哈希表map来存储原图中的节点和新图中的节点的一一映射。map的作用在于替代bfs和dfs中的visit数组，一旦map中出现了映射关系，就说明已经复制完成，也就是已经访问过了。

BFS

# Definition for a undirected graph node
# class UndirectedGraphNode:
#     def __init__(self, x):
#         self.label = x
#         self.neighbors = []

class Solution:
    # @param node, a undirected graph node
    # @return a undirected graph node
    def cloneGraph(self, node):
        if not node:
            return None
        queue = []
        dic = {}
        newhead = UndirectedGraphNode(node.label)
        dic[node] = newhead
        queue.append(node)
        while queue:
            curr = queue.pop()
            for neighbor in curr.neighbors:
                if neighbor not in dic:
                    copy = UndirectedGraphNode(neighbor.label)
                    dic[curr].neighbors.append(copy)
                    dic[neighbor] = copy
                    queue.append(neighbor)
                else:
                    dic[curr].neighbors.append(dic[neighbor])
        return newhead

DFS

# Definition for a undirected graph node
# class UndirectedGraphNode:
#     def __init__(self, x):
#         self.label = x
#         self.neighbors = []

class Solution:
    # @param node, a undirected graph node
    # @return a undirected graph node
    def cloneGraph(self, node):
        if not node:
            return None
        return self.dfs(node, {})
    
    def dfs(self, input, dic):
        if input in dic:
            return dic[input]
        output = UndirectedGraphNode(input.label)
        dic[input] = output
        for neighbor in input.neighbors:
            output.neighbors.append(self.dfs(neighbor, dic))
        return output

199. 二叉树的右视图

题目描述

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

解题思路

按层次遍历，没层取最右边元素。

BFS

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def rightSideView(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        queue = [root]
        res = []
        while queue:
            temp = []
            for i in range(len(queue)):
                cur = queue.pop(0)
                temp.append(cur.val)
                if cur.left:
                    queue.append(cur.left)
                if cur.right:
                    queue.append(cur.right)
            if temp:
                res.append(temp[-1])
        return res

DFS

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def rightSideView(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        res = []
        self.dfs(root, 0, res)
        return [level[-1] for level in res]
    
    def dfs(self, root, level, res):
        if not root:
            return []
        if level == len(res):
            res.append([])
        res[level].append(root.val)
        if root.left:
            self.dfs(root.left, level+1, res)
        if root.right:
            self.dfs(root.right, level+1, res)

200. 岛屿的个数

题目描述

给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

示例 2:

解题思路

给定由0和1组成的二维数组，求1的连通块。

BFS 超时

class Solution(object):
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        if len(grid) == 0:
            return 0
        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == '1':
                    self.bfs(grid, i, j)
                    count += 1
        return count
    
    def bfs(self, grid, i, j):
        queue = collections.deque()
        queue.append((i,j))
        grid[i][j] = '#'
        direction = [(0,1), (0,-1), (1,0), (-1,0)]
        while queue:
            i, j = queue.popleft()
            for d in direction:
                r, c = i + d[0], i + d[1]
                if 0 <= r < len(grid) and 0 <= c < len(grid[0]) and grid[r][c] == '1':
                    grid[r][c] == '#'
                    queue.append((r, c))

DFS

class Solution(object):
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        if len(grid) == 0:
            return 0
        count = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == '1':
                    self.dfs(grid, i, j)
                    count += 1
        return count
    def dfs(self, grid, i, j):
        if 0 <= i < len(grid) and 0 <= j < len(grid[0]) and grid[i][j] == '1':
            grid[i][j] = '#'
            self.dfs(grid, i-1, j)
            self.dfs(grid, i+1, j)
            self.dfs(grid, i, j-1)
            self.dfs(grid, i, j+1)

207. 课程表

题目描述

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

**输入:** 2, [[1,0]] 
**输出: **true
**解释:** 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

**输入:** 2, [[1,0],[0,1]]
**输出: **false
**解释:** 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

说明:

输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。

提示:

这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

解题思路

使用拓扑排序。
在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

每个顶点出现且只出现一次。
若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

BFS方法：
我们开始先根据输入来建立这个有向图，并将入度数组也初始化好。然后我们定义一个 queue 变量，将所有入度为0的点放入队列中，然后开始遍历队列，从 graph 里遍历其连接的点，每到达一个新节点，将其入度减一，如果此时该点入度为0，则放入队列末尾。直到遍历完队列中所有的值，若此时还有节点的入度不为0，则说明环存在，返回 false，反之则返回 true。


class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        
        graph = collections.defaultdict(list)
        indegree = [0] * numCourses

        # 使用邻接表存储图
        for u, v in prerequisites:
            graph[v].append(u)
            indegree[u] += 1

        # 保存入度为0的课表
        queue = []
        for i in range(numCourses):
            if indegree[i] == 0:
                queue.append(i)

        while queue:
            node = queue.pop(0)
            if node not in graph:
                continue
            for i in graph[node]:
                indegree[i] -= 1
                if indegree[i] == 0:
                    queue.append(i)

        for i in range(numCourses):
            if indegree[i] != 0:
                return False

        return True

DFS：
这个方法是，我们每次找到一个新的点，判断从这个点出发是否有环。
具体做法是使用一个visited数组，当visited[i]值为0，说明还没判断这个点；当visited[i]值为1，说明当前的循环正在判断这个点；当visited[i]值为2，说明已经判断过这个点，含义是从这个点往后的所有路径都没有环，认为这个点是安全的。

那么，我们对每个点出发都做这个判断，检查这个点出发的所有路径上是否有环，如果判断过程中找到了当前的正在判断的路径，说明有环；找到了已经判断正常的点，说明往后都不可能存在环，所以认为当前的节点也是安全的。如果当前点是未知状态，那么先把当前点标记成正在访问状态，然后找后续的节点，直到找到安全的节点为止。最后如果到达了无路可走的状态，说明当前节点是安全的。

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        
        graph = collections.defaultdict(list)

        # 使用邻接表存储图
        for u, v in prerequisites:
            graph[v].append(u)

        visited = [0] * numCourses
        for i in range(numCourses):
            if not self.judge(graph, visited, i):
                return False
        return True

    def judge(self, graph, visited, i):
        if visited[i] == 1:
            return False
        if visited[i] == 2:
            return True
        visited[i] = 1

        for j in graph[i]:
            if not self.judge(graph, visited, j):
                return False
        visited[i] = 2
        return True

210. 课程表 II

题目描述

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1:

1
2
3

**输入:** 2, [[1,0]] 
**输出: **[0,1]
**解释:** 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2:

**输入:** 4, [[1,0],[2,0],[3,1],[3,2]]
**输出: **[0,1,2,3] or [0,2,1,3]
**解释:** 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
``` 

**说明:**

1. 输入的先决条件是由**边缘列表**表示的图形，而不是邻接矩阵。详情请参见[图的表示法](http://blog.csdn.net/woaidapaopao/article/details/51732947)。
2. 你可以假定输入的先决条件中没有重复的边。

**提示:**

1. 这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
2. [通过 DFS 进行拓扑排序](https://www.coursera.org/specializations/algorithms) - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
3. 
拓扑排序也可以通过 [BFS](https://baike.baidu.com/item/%E5%AE%BD%E5%BA%A6%E4%BC%98%E5%85%88%E6%90%9C%E7%B4%A2/5224802?fr=aladdin&amp;fromid=2148012&amp;fromtitle=%E5%B9%BF%E5%BA%A6%E4%BC%98%E5%85%88%E6%90%9C%E7%B4%A2) 完成。

### 解题思路

拓扑排序
BFS
```python
import collections
class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: List[int]
        """

        graph = collections.defaultdict(list)
        indegrees = [0] * numCourses

        for u, v in prerequisites:
            graph[v].append(u)
            indegrees[u] += 1
        queue = []
        for i in range(numCourses):
            if indegrees[i] == 0:
                queue.append(i)
        res = []
        while queue:
            node = queue.pop(0)
            res.append(node)
            for t in graph[node]:
                indegrees[t] -= 1
                if indegrees[t] == 0:
                    queue.append(t)

        return res if len(res) == numCourses else []

DFS

import collections
class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: List[int]
        """

        graph = collections.defaultdict(list)

        for u, v in prerequisites:
            graph[v].append(u)

        res = []
        visited = [0] * numCourses

        for i in range(numCourses):
            if not self.judge(graph, visited, i, res):
                return []

        return res[::-1] if len(res) == numCourses else []

    def judge(self, graph, visited, i, res):
        if visited[i] == 1:
            return False
        if visited[i] == 2:
            return True
        visited[i] = 1
        for j in graph[i]:
            if not self.judge(graph, visited, j, res):
                return False
        visited[i] = 2
        res.append(i)
        return True

279. 完全平方数

题目描述

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2：

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

解题思路

使用DFS，如n=12，首先计算出可能存在的平方数candidate = [1,4,9]，然后对当前残差及candidate进行遍历，直到残差等于candidate，则返回。

class Solution:
    def numSquares(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n < 0:
            return 0
        if n <= 1:
            return 1
        candidate = []
        i = 1
        while i*i <= n:
            candidate.append(i*i)
            i += 1
        count = 0
        toCheck = {n}
        while toCheck:
            count += 1
            temp = set()
            for residue in toCheck:
                for cand in candidate:
                    if residue == cand:
                        return count
                    if residue < cand:
                        break
                    temp.add(residue-cand)
            toCheck = temp
        return count

if __name__ == '__main__':
    result = Solution().numSquares(12)
    print(result)

547. 朋友圈

题目描述

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:

输入: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出: 2 
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

示例 2:

输入: 
[[1,1,0],
 [1,1,1],
 [0,1,1]]
输出: 1
说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

注意：

1
2
3

N 在[1,200]的范围内。
对于所有学生，有M[i][i] = 1。
如果有M[i][j] = 1，则有M[j][i] = 1。

解题思路

思路1 DFS

class Solution(object):
    def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        
        if len(M) == 0:
            return 0
        
        res = 0
        visited = [False]*len(M)
        for i in range(len(M)):
            if not visited[i]:
                res += 1
                self.dfs(M, i, visited)
        return res
    
    def dfs(self, M, i, visited):
        visited[i] = True
        for j in range(len(M)):
            if M[i][j] == 1 and not visited[j]:
                self.dfs(M, j, visited)

思路2 并查集

核心思想是初始时给每一个对象都赋上不同的标签，然后对于属于同一类的对象，在root中查找其标签，如果不同，那么将其中一个对象的标签赋值给另一个对象，注意root数组中的数字跟数字的坐标是有很大关系的，root存的是属于同一组的另一个对象的坐标，这样通过getRoot函数可以使同一个组的对象返回相同的值。

class Solution(object):
    def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        
        if len(M) == 0:
            return 0
        
        res = len(M)
        root = [0] * len(M)
        for i in range(len(M)):
            root[i] = i
        
        for i in range(len(M)):
            for j in range(i+1, len(M)):
                if M[i][j] == 1:
                    p1 = self.getRoot(root, i)
                    p2 = self.getRoot(root, j)
                    if p1!=p2:
                        res -= 1
                        root[p2] = p1
        return res
    
    def getRoot(self, root, i):
        while i != root[i]:
            root[i] = root[root[i]]
            i = root[i]
        return i

搜索

广度优先搜索(BFS)

无向图的广度优先搜索

有向图的广度优先搜索

深度优先搜索(DFS)

无向图的深度优先搜索

有向图的深度优先搜索

127. 单词接龙

解题思路

130. 被围绕的区域

解题思路

133. 克隆图

解题思路

199. 二叉树的右视图

解题思路

200. 岛屿的个数

解题思路

207. 课程表

解题思路

210. 课程表 II

279. 完全平方数

解题思路

547. 朋友圈

解题思路