本系列为Leetcode刷题笔记,刷题平台为Leetcode中文站, 刷题按Tag分类。本系列题解汇总如下 (持续更新…):
本文主要是数学相关题目题解总结。
[TOC]
2. 两数相加
题目描述
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:1
2
3输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
解题思路
使用哨兵节点,设置进位carry,直接相加,当进位为1时加到下一位。
1 | # Definition for singly-linked list. |
第一次写的思路:先求和,在构建链表。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
if not l2:
return l1
if not l1:
return l2
num1, num2 = 0, 0
base = 1
while l1:
num1 += l1.val * base
base *= 10
l1 = l1.next
base = 1
while l2:
num2 += l2.val*base
base *= 10
l2 = l2.next
num = num1 + num2
if num == 0:
root = ListNode(0)
return root
return self.helper(num)
def helper(self, num):
if num == 0:
return None
root = ListNode(num % 10)
root.next = self.helper(num // 10)
return root
7. 整数反转
题目描述
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
示例 1:1
2输入: 123
输出: 321
示例 2:1
2输入: -123
输出: -321
示例 3:1
2输入: 120
输出: 21
注意:1
假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [−231, 231 − 1]。请根据这个假设,如果反转后整数溢出那么就返回 0。
解题思路
1 | class Solution(object): |
8. 字符串转换整数 (atoi)
题目描述
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,qing返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
示例 1:1
2输入: "42"
输出: 42
示例 2:1
2
3
4输入: " -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:1
2
3输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ,因为它的下一个字符不为数字。
示例 4:1
2
3
4输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
因此无法执行有效的转换。
示例 5:1
2
3
4输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。
解题思路
一个一个条件判断。。。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution(object):
def myAtoi(self, str):
"""
:type str: str
:rtype: int
"""
if not str:
return 0
i = 0
while i < len(str) and str[i] == ' ':
i += 1
if i == len(str) or str[i] not in '1234567890+-':
return 0
flag = 1
if str[i] in '+-':
if i == len(str)-1 or str[i+1] not in '1234567890':
return 0
elif str[i] == '-':
flag = -1
i = i+1
start = i
end = start
while end < len(str) and str[end] in '1234567890':
end += 1
res = flag*int(str[start:end])
if res > 2**31-1:
return 2**31-1
if res < -2**31:
return -2**31
return res
9. 回文数
题目描述
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
示例 1:1
2输入: 121
输出: true
示例 2:1
2
3输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:1
2
3
4输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。
进阶:
你能不将整数转为字符串来解决这个问题吗?
解题思路
1 | class Solution(object): |
1 | class Solution(object): |
12. 整数转罗马数字
题目描述
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。1
2
3
4
5
6
7
8字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个整数,将其转为罗马数字。输入确保在 1 到 3999 的范围内。
示例 1:1
2输入: 3
输出: "III"
示例 2:1
2输入: 4
输出: "IV"
示例 3:1
2输入: 9
输出: "IX"
示例 4:1
2
3输入: 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.
示例 5:1
2
3输入: 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.
解题思路
1 | class Solution(object): |
13. 罗马数字转整数
题目描述
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。1
2
3
4
5
6
7
8字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:1
2输入: "III"
输出: 3
示例 2:1
2输入: "IV"
输出: 4
示例 3:1
2输入: "IX"
输出: 9
示例 4:1
2
3输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:1
2
3输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
解题思路
1 | class Solution(object): |
1 | class Solution(object): |
29. 两数相除
题目描述
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
示例 1:1
2输入: dividend = 10, divisor = 3
输出: 3
示例 2:1
2输入: dividend = 7, divisor = -3
输出: -2
说明:1
2
3被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。
解题思路
通过位运算模拟乘2的操作,加快扩大divisor的速度。
使用两层while,外层用来控制最终跳出循环,同时初始化逼近的间隔;内层通过不断的乘2用来加快逼近速度。属于二分查找的变种。
1 | class Solution(object): |
一层循环超出时间限制1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution(object):
def divide(self, dividend, divisor):
"""
:type dividend: int
:type divisor: int
:rtype: int
"""
if dividend == 0:
return 0
flag = 1 if (dividend < 0) is (divisor < 0) else -1
dividend, divisor = abs(dividend), abs(divisor)
res = 0
while dividend >= divisor:
res += 1
dividend -= divisor
res = res*flag
if res > 2**31-1:
return 2**31-1
if res < -2**31:
return -2**31
return res
43. 字符串相乘
题目描述
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
示例 1:1
2输入: num1 = "2", num2 = "3"
输出: "6"
示例 2:1
2输入: num1 = "123", num2 = "456"
输出: "56088"
说明:1
2
3
4num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头,除非是数字 0 本身。
不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
解题思路
按照乘法竖式计算,将num1和num2翻转,用num1中的每一个数和num2进行相乘,乘法过程中考虑进位和位数。
1 | class Solution(object): |
二刷。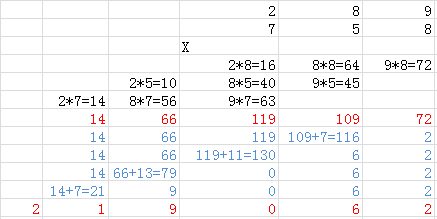
1 | class Solution(object): |
1 |
|
50. Pow(x, n)
题目描述
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:1
2输入: 2.00000, 10
输出: 1024.00000
示例 2:1
2输入: 2.10000, 3
输出: 9.26100
示例 3:1
2
3输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
说明:1
2-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
解题思路
直接乘,超时。
1 | class Solution(object): |
二分求幂,递归。
- 如果n=0,返回1;
- 如果n为负数,相当于求(1.0/x)^(-n)。
- 如果n为正奇数,相当于求 x (x^2)^(n//2);
- 如果n为正偶数,相当于求 (x^2)^(n//2)。
1 | class Solution(object): |
二分求幂,迭代。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution(object):
def myPow(self, x, n):
"""
:type x: float
:type n: int
:rtype: float
"""
if n == 0:
return 1.0
flag = (n<0)
n = abs(n)
res = 1
while n:
if n%2 == 1:
res *= x
n >>= 1
x *=x
if flag:
res = 1.0/res
return res
60. 第k个排列
题目描述
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:1
2
3
4
5
6"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k,返回第 k 个排列。
说明:1
2给定 n 的范围是 [1, 9]。
给定 k 的范围是[1, n!]。
示例 1:1
2输入: n = 3, k = 3
输出: "213"
示例 2:1
2输入: n = 4, k = 9
输出: "2314"
解题思路
以n=4, k=9为例,初始化k=k-1=8。
- 最高位可取数字为[1,2,3,4],每一个取值都有3!=6种取法,那么第9个下标为k//(n-1)!=8//6=1,即2,可取数字删去2更新为[1,3,4],k=k%(n-1)!=2;
- 次高位可取数字为[1,3,4],每一个取值都有2!=2种取法,那么第九个下标为k//(n-1-1)!=2//2=1,即3,可取数字删去3更新为[1,4],k=k%(n-1-1)!=0;
- 第三位可取数字为[1,4],每一个取值都有1!=1中取法,那么第九个下标为k//(n-1-1-1)!=0//1=0,即1,可取数字删去1更新为[4],k=k%(n-1-1-1)=0;
- 第四位为[4]。
1 | class Solution(object): |
66. 加一
题目描述
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储一个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:1
2
3输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:1
2
3输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
解题思路
数九。从最后一位开始遍历,若当前遍历的值为9,则置为0;如果不是9,则当前位加1跳出循环;最后判断最高位是否为0,若为0,则需要在增加数组长度,即在最高位之前插入1。
1 | class Solution(object): |
采用进位。初始化进位为0,首先对最后一位加1操作,从后向前遍历,当当前位加上进位等于10时,将改为置0,进位置1,如小于10,则将进位置0,跳出循环。
1 | class Solution(object): |
一刷。
1 | class Solution(object): |
67. 二进制求和
题目描述
给定两个二进制字符串,返回他们的和(用二进制表示)。
输入为非空字符串且只包含数字 1 和 0。
示例 1:1
2输入: a = "11", b = "1"
输出: "100"
示例 2:1
2输入: a = "1010", b = "1011"
输出: "10101"
解题思路
设置当前位和plus,从后向前遍历,将每一位(plus%2)加入到结果中,将进位(plus//2)赋给下一次迭代位和plus。
1 | class Solution(object): |
69. x 的平方根
题目描述
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:1
2输入: 4
输出: 2
示例 2:1
2
3
4输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。
解题思路
二分查找。
1 | class Solution(object): |
166. 分数到小数
题目描述
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以字符串形式返回小数。
如果小数部分为循环小数,则将循环的部分括在括号内。
示例 1:1
2输入: numerator = 1, denominator = 2
输出: "0.5"
示例 2:1
2输入: numerator = 2, denominator = 1
输出: "2"
示例 3:1
2输入: numerator = 2, denominator = 3
输出: "0.(6)"
解题思路
先处理分子,分母为零,负数的情况。然后使用字典将余数保存起来,当余数不为零时,在结果后加小数位数,当余数重复出现时,找到最开始重复的位置,加括号返回。
1 | class Solution(object): |
168. Excel表列名称
题目描述
给定一个正整数,返回它在 Excel 表中相对应的列名称。
例如,1
2
3
4
5
6
7
81 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
示例 1:1
2输入: 1
输出: "A"
示例 2:1
2输入: 28
输出: "AB"
示例 3:1
2输入: 701
输出: "ZY"
解题思路
字母26为一个周期。
1 | class Solution(object): |
171. Excel表列序号
题目描述
给定一个Excel表格中的列名称,返回其相应的列序号。
例如,1
2
3
4
5
6
7
8A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
示例 1:1
2输入: "A"
输出: 1
示例 2:1
2输入: "AB"
输出: 28
示例 3:1
2输入: "ZY"
输出: 701
解题思路
字母26为一个周期。
1 | class Solution(object): |
1 | class Solution(object): |
172. 阶乘后的零
题目描述
给定一个整数 n,返回 n! 结果尾数中零的数量。
示例 1:1
2
3输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:1
2
3输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。
解题思路
- 6!=[123456],其中25才有0,所以可以抛开其他数据,只看2,5出现的次数;
- 10!=[12345678910],有2,5组成的有2,4(22),5,6(23),8(222),10(25),一个2和一个5配对产生一个0,所以有两个配对有两个0。由于2一定比5多,只对5计数就可以了。
1 | class Solution(object): |
202. 快乐数
题目描述
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。
示例:1
2
3
4
5
6
7输入: 19
输出: true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
解题思路
1 | class Solution(object): |
204. 计数质数
题目描述
统计所有小于非负整数 n 的质数的数量。
示例:1
2
3输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
解题思路
超时1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution(object):
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
if n <= 2:
return 0
res = 0
for i in range(2, n):
flag = 1
for j in range(2, i):
if i % j == 0:
flag = 0
break
if flag:
res += 1
return res
厄拉多塞筛法.
比如说求20以内质数的个数,首先0,1不是质数.2是第一个质数,然后把20以内所有2的倍数划去.2后面紧跟的数即为下一个质数3,然后把3所有的倍数划去.3后面紧跟的数即为下一个质数5,再把5所有的倍数划去.以此类推.
首先生成了一个全部为1的列表
res= [1] * n
因为0和1不是质数,所以列表的前两个位置赋值为0
res[0],res[1] = 0,0
此时从index = 2开始遍历,res[2]==1,即表明第一个质数为2,然后将2的倍数对应的索引,全部赋值为0.
此时res[3] == 1,即表明下一个质数为3,同样划去3的倍数.以此类推.
1 | class Solution(object): |
223. 矩形面积
题目描述
在二维平面上计算出两个由直线构成的矩形重叠后形成的总面积。
每个矩形由其左下顶点和右上顶点坐标表示,如图所示。

示例:1
2输入: -3, 0, 3, 4, 0, -1, 9, 2
输出: 45
说明: 假设矩形面积不会超出 int 的范围。
解题思路
分两种情况,第一种是不重叠,第二种重叠1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution(object):
def computeArea(self, A, B, C, D, E, F, G, H):
"""
:type A: int
:type B: int
:type C: int
:type D: int
:type E: int
:type F: int
:type G: int
:type H: int
:rtype: int
"""
if E >= C or A >= G or F >= D or B >= H:
return (C-A)*(D-B) + (G-E)*(H-F)
else:
return (C-A)*(D-B) + (G-E)*(H-F) - (min(G,C)-max(A,E)) * (min(D,H)-max(B,F))
231. 2的幂
题目描述
1 | 给定一个整数,编写一个函数来判断它是否是 2 的幂次方。 |
解题思路
2的幂的二进制中只有一位是1.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution(object):
def isPowerOfTwo(self, n):
"""
:type n: int
:rtype: bool
"""
if n == 0:
return False
res = 0
while n:
if n & 1:
res += 1
if res >= 2:
return False
n >>= 1
return True
2的幂的数 n和(n-1)相与一定是0,不为0则不是2的幂
如
8(0000 1000) & 7 (0000 0111) ==0
24(0001 1000) & 23 (0001 0111) != 0
1 | class Solution(object): |
258. 各位相加
题目描述
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。
示例:1
2
3输入: 38
输出: 2
解释: 各位相加的过程为:3 + 8 = 11, 1 + 1 = 2。 由于 2 是一位数,所以返回 2。
进阶:
- 你可以不使用循环或者递归,且在 O(1) 时间复杂度内解决这个问题吗?
解题思路
暴力1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution(object):
def addDigits(self, num):
"""
:type num: int
:rtype: int
"""
if num <= 9:
return num
while num >= 10:
lastn = num
nextn = 0
while lastn:
nextn += lastn % 10
lastn //= 10
num = nextn
return num
余9法。1
2
3
4
5
6
7
8
9
10
11假设输入的数字是一个5位数字num,则num的各位分别为a、b、c、d、e。
有如下关系:num = a * 10000 + b * 1000 + c * 100 + d * 10 + e
即:num = (a + b + c + d + e) + (a * 9999 + b * 999 + c * 99 + d * 9)
因为 a * 9999 + b * 999 + c * 99 + d * 9 一定可以被9整除,因此num模除9的结果与 a + b + c + d + e 模除9的结果是一样的。
对数字 a + b + c + d + e 反复执行同类操作,最后的结果就是一个 1-9 的数字加上一串数字,最左边的数字是 1-9 之间的,右侧的数字永远都是可以被9整除的。
这道题最后的目标,就是不断将各位相加,相加到最后,当结果小于10时返回。因为最后结果在1-9之间,得到9之后将不会再对各位进行相加,因此不会出现结果为0的情况。因为 (x + y) % z = (x % z + y % z) % z,又因为 x % z % z = x % z,因此结果为 (num - 1) % 9 + 1,只模除9一次,并将模除后的结果加一返回。
参考1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution(object):
def addDigits(self, num):
"""
:type num: int
:rtype: int
"""
if num <= 9:
return num
if num % 9 == 0:
return 9
else:
return num % 9
263. 丑数
题目描述
编写一个程序判断给定的数是否为丑数。
丑数就是只包含质因数 2, 3, 5 的正整数。
示例 1:1
2
3输入: 6
输出: true
解释: 6 = 2 × 3
示例 2:1
2
3输入: 8
输出: true
解释: 8 = 2 × 2 × 2
示例 3:1
2
3输入: 14
输出: false
解释: 14 不是丑数,因为它包含了另外一个质因数 7。
说明:1
21 是丑数。
2 输入不会超过 32 位有符号整数的范围: [−231, 231 − 1]。
解题思路
不断的除5,3,2,最后为1则为丑数
1 | class Solution(object): |
264. 丑数 II
题目描述
编写一个程序,找出第 n 个丑数。
丑数就是只包含质因数 2, 3, 5 的正整数。
示例:1
2
3输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
- 1 是丑数。
- n 不超过1690。
解题思路
1 | class Solution(object): |
313. 超级丑数
题目描述
编写一段程序来查找第 n 个超级丑数。
超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。
示例:1
2
3输入: n = 12, primes = [2,7,13,19]
输出: 32
解释: 给定长度为 4 的质数列表 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
说明:1
2
3
41 是任何给定 primes 的超级丑数。
给定 primes 中的数字以升序排列。
0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000 。
第 n 个超级丑数确保在 32 位有符整数范围内。
解题思路
1 | class Solution(object): |
319. 灯泡开关
题目描述
初始时有 n 个灯泡关闭。 第 1 轮,你打开所有的灯泡。 第 2 轮,每两个灯泡你关闭一次。 第 3 轮,每三个灯泡切换一次开关(如果关闭则开启,如果开启则关闭)。第 i 轮,每 i 个灯泡切换一次开关。 对于第 n 轮,你只切换最后一个灯泡的开关。 找出 n 轮后有多少个亮着的灯泡。
示例:1
2
3
4
5
6
7
8
9输入: 3
输出: 1
解释:
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].
你应该返回 1,因为只有一个灯泡还亮着。
解题思路
暴力超时。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution(object):
def bulbSwitch(self, n):
"""
:type n: int
:rtype: int
"""
if n == 0:
return 0
if n <= 3:
return 1
dp = [1] * n
for i in range(1, n):
for i in range(i, n, i+1):
dp[i] *= -1
return dp.count(1)
数学法。开平方?1
2
3
4
5
6
7
8class Solution(object):
def bulbSwitch(self, n):
"""
:type n: int
:rtype: int
"""
return int(n**0.5)
326. 3的幂
题目描述
给定一个整数,写一个函数来判断它是否是 3 的幂次方。
示例 1:
输入: 27
输出: true
示例 2:
输入: 0
输出: false
示例 3:
输入: 9
输出: true
示例 4:
输入: 45
输出: false
进阶:
你能不使用循环或者递归来完成本题吗?
解题思路
1 | class Solution(object): |
365. 水壶问题
题目描述
有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升 水。
你允许:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1: (From the famous “Die Hard” example)1
2输入: x = 3, y = 5, z = 4
输出: True
示例 2:1
2输入: x = 2, y = 6, z = 5
输出: False
解题思路
1 | 这是一道脑筋急转弯题,我想很多人以前应该听过这道题目,有一个容量为3升和一个容量为5升的水罐,问我们如何准确的称出4升的水。我想很多人都知道怎么做,先把5升水罐装满水,倒到3升水罐里,这时5升水罐里还有2升水,然后把3升水罐里的水都倒掉,把5升水罐中的2升水倒入3升水罐中,这时候把5升水罐解满,然后往此时有2升水的3升水罐里倒水,这样5升水罐倒出1升后还剩4升即为所求。这个很多人都知道,但是这道题随意给我们了三个参数,问有没有解法,这就比较难了。这里我就照搬网上大神的讲解吧: |
1 | class Solution(object): |
367. 有效的完全平方数
题目描述
给定一个正整数 num,编写一个函数,如果 num 是一个完全平方数,则返回 True,否则返回 False。
说明:不要使用任何内置的库函数,如 sqrt。
示例 1:1
2输入:16
输出:True
示例 2:1
2输入:14
输出:False
解题思路
二分搜索1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution(object):
def isPerfectSquare(self, num):
"""
:type num: int
:rtype: bool
"""
if num == 0:
return False
left, right = 1, int(num**0.5)+1
while left <= right:
mid = left + (right-left)//2
if mid*mid == num:
return True
elif mid*mid > num:
right = mid-1
else:
left = mid+1
return False
372. 超级次方
题目描述
你的任务是计算 ab 对 1337 取模,a 是一个正整数,b 是一个非常大的正整数且会以数组形式给出。
示例 1:1
2输入: a = 2, b = [3]
输出: 8
示例 2:1
2输入: a = 2, b = [1,0]
输出: 1024
解题思路
二分求幂1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution(object):
def superPow(self, a, b):
"""
:type a: int
:type b: List[int]
:rtype: int
"""
res = 1
for n in b:
res = self.pow(res, 10) * self.pow(a, n) % 1337
return res
def pow(self, x, n):
if x == 1 or n == 0:
return 1
if n % 2:
return self.pow(x, n-1) * x % 1337
else:
return self.pow(x*x%1337, n//2) % 1337
396. 旋转函数
题目描述
给定一个长度为 n 的整数数组 A 。
假设 Bk 是数组 A 顺时针旋转 k 个位置后的数组,我们定义 A 的“旋转函数” F 为:1
F(k) = 0 * Bk[0] + 1 * Bk[1] + ... + (n-1) * Bk[n-1]。
计算F(0), F(1), …, F(n-1)中的最大值。
注意:
可以认为 n 的值小于 105。
示例:1
2
3
4
5
6
7
8A = [4, 3, 2, 6]
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。
解题思路
看了数据规模是10^5,可以知道时间复杂度是O(N)量级,这就难办了。我们为了找规律,先把具体的数字抽象为A,B,C,D,那么我们可以得到:1
2
3
4
5
6
7
8
9
10
11
12
F(0) = 0A + 1B + 2C +3D
F(1) = 0D + 1A + 2B +3C
F(2) = 0C + 1D + 2A +3B
F(3) = 0B + 1C + 2D +3A
那么,我们通过仔细观察,我们可以得出下面的规律:1
2
3
4
5
6
7
8
9
F(1) = F(0) + sum - 4D
F(2) = F(1) + sum - 4C
F(3) = F(2) + sum - 4B
那么我们就找到规律了,1
F(i) = F(i-1) + sum - n * A[n-i],
是个递推公式。我们最后求的是这个所有F(i)中的最大值。
时间复杂度是O(N),空间复杂度是O(1).
参考1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution(object):
def maxRotateFunction(self, A):
"""
:type A: List[int]
:rtype: int
"""
sumA = sum(A)
f = sum(i*A[i] for i in range(len(A)))
res = f
for i in range(1, len(A)):
f = f + sumA - len(A)*A[-i]
res = max(res, f)
return res
397. 整数替换
题目描述
给定一个正整数 n,你可以做如下操作:
- 如果 n 是偶数,则用 n / 2替换 n。
- 如果 n 是奇数,则可以用 n + 1或n - 1替换 n。
n 变为 1 所需的最小替换次数是多少?
示例 1:1
2
3
4
5
6
7
8输入:
8
输出:
3
解释:
8 -> 4 -> 2 -> 1
示例 2:1
2
3
4
5
6
7
8
9
10输入:
7
输出:
4
解释:
7 -> 8 -> 4 -> 2 -> 1
或
7 -> 6 -> 3 -> 2 -> 1
解题思路
思路1:递归,速度很慢1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution(object):
def integerReplacement(self, n):
"""
:type n: int
:rtype: int
"""
if n <= 1:
return 0
if n == 2:
return 1
if n % 2 == 0:
return 1 + self.integerReplacement(n//2)
else:
return 1 + min(self.integerReplacement(n-1), self.integerReplacement(n+1))
思路2:位运算,速度很快
当n是偶数时,直接除2;
当n是奇数时,-1还是+1?奇数二进制数一定是01或者11结尾,如果把一个奇数化为4的倍数,变成1的步骤会更少(3除外):
15->16->8->4->2->1
15->14->7->6->3->2->1
因此:如果结尾是01,减1,如果结尾时11,加1,3的时候直接减1。
1 | class Solution(object): |
400. 第N个数字
题目描述
在无限的整数序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …中找到第 n 个数字。
注意:
n 是正数且在32为整形范围内 ( n < 231)。
示例 1:1
2
3
4
5输入:
3
输出:
3
示例 2:1
2
3
4
5
6
7
8输入:
11
输出:
0
说明:
第11个数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是0,它是10的一部分。
解题思路
一位数字有9个,有9位;
2位数字有9*10=90个,有2*90=180位;
3位数字有9*100=900个,有3*900=2700位;
首先找到n是几位数字,然后找到n是所在位数的第几个数字,最后求在这个数字的第几位上。
1 | class Solution(object): |
892. 三维形体的表面积
题目描述
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
示例 1:
**输入:**[[2]]
**输出:**10
示例 2:
**输入:**[[1,2],[3,4]]
**输出:**34
示例 3:
**输入:**[[1,0],[0,2]]
**输出:**16
示例 4:
**输入:**[[1,1,1],[1,0,1],[1,1,1]]
**输出:**32
示例 5:
**输入:**[[2,2,2],[2,1,2],[2,2,2]]
**输出:**46
提示:
1 <= N <= 500 <= grid[i][j] <= 50
解题思路
对矩阵进行遍历,分别求每个位置的表面积,当某个位置垒了n(n>0)个正方体,则其表面积为4*n+2 (四个侧面+上下两个面),如果其前面或者上面有立方体存在,则会产生重叠,需要减去,重叠部分为两者较矮的那堆立方体个数乘以2。
1 | class Solution(object): |

