Leetcode题解 - 回溯算法

本系列为Leetcode刷题笔记，刷题平台为Leetcode中文站， 刷题按Tag分类。本系列题解汇总如下 (持续更新…)：

本文主要是回溯算法相关题目题解总结。

[TOC]

回溯算法

回溯算法属于DFS。在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回（也就是递归返回），尝试别的路径。

• 普通DFS主要用于可达性问题，这种问题只需要执行到特定的位置然后返回即可；
• 而Backtracking主要用于求解排列组合问题，例如有 { ‘a’,’b’,’c’ } 三个字符，求解所有由这三个字符排列得到的字符串，这种问题在执行到特定的位置返回之后还会继续执行求解过程。

Backtracking的基本思想是：

• 从一条路往前走，能进则进，不能进则退回来，换一条路再试。
• 八皇后问题就是回溯算法的典型，第一步按照顺序放一个皇后，然后第二步符合要求放第2个皇后，如果没有位置符合要求，那么就要改变第一个皇后的位置，重新放第2个皇后的位置，直到找到符合条件的位置就可以了。
• 回溯在迷宫搜索中使用很常见，就是这条路走不通，然后返回前一个路口，继续下一条路。
• 回溯算法说白了就是穷举法。

因为 Backtracking 不是立即就返回，而要继续求解，因此在程序实现时，需要注意对元素的标记问题：

• 在访问一个新元素进入新的递归调用时，需要将新元素标记为已经访问，这样才能在继续递归调用时不用重复访问该元素；
• 但是在递归返回时，需要将元素标记为未访问，因为只需要保证在一个递归链中不同时访问一个元素，可以访问已经访问过但是不在当前递归链中的元素。

17. 电话号码的字母组合

题目描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

输入：”23”
输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

说明:

尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

解题思路

回溯。要求所有位置都要有字母，即组合的长度为数字的长度。

class Solution(object):
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
        if len(digits) == 0:
            return []
        dic = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
        res = []
        self.dfs(digits, 0, '', dic, res)
        return res
    def dfs(self, digits, index, path, dic, res):
        if len(path) == len(digits):
            if path:
                res.append(path)
            return
        if digits[index] not in dic:
            return []
        for j in dic[digits[index]]:
            self.dfs(digits, index+1, path+j, dic, res)

class Solution(object):
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
        
        if len(digits) == 0:
            return []
        
        Dict = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
        
        strs = []
        for x in digits:
            strs.append(Dict[x])
        
        res = []
        self.dfs(strs, 0, '', res)
        return res
    
    def dfs(self, strs, index, path, res):
        if len(path) == len(strs):
            res.append(path)
            return
        
        for j in strs[index]:
            self.dfs(strs, index+1, path+j, res)

22. 括号生成

题目描述

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

解题思路

回溯。如果左括号还有剩余，则放置左括号，如果有括号剩余数大于左括号，则可以放置有括号，停止条件为所有括号全部放置完。

class Solution(object):
    def generateParenthesis(self, n):
        """
        :type n: int
        :rtype: List[str]
        """
        if n <= 0:
            return []
        res = []
        self.dfs(n, n, '', res)
        return res
    def dfs(self, left, right, path, res):
        if left == 0 and right == 0:
            res.append(path)
            return
        if left > 0:
            self.dfs(left-1, right, path+'(', res)
        if left < right:
            self.dfs(left, right-1, path+')', res)

39. 组合总和

题目描述

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

• 说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

• 示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]

• 示例 2:

  输入: candidates = [2,3,5], target = 8,
  所求解集为:
  [
  [2,2,2,2],
  [2,3,3],
  [3,5]
  ]

解题思路

先进行排序在dfs。

class Solution(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        if len(candidates) == 0:
            return []
        res = []
        candidates.sort()
        self.dfs(candidates, target, 0, [], res)
        return res
    def dfs(self, candidates, residue, start, templist, res):
        if residue == 0:
            res.append(templist)
            return
        for i in range(start, len(candidates)):
            if candidates[i] > residue:
                return
            self.dfs(candidates, residue-candidates[i], i, templist+[candidates[i]], res)

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if (candidates.length==0)
            return res;
        Arrays.sort(candidates);
        dfs(candidates, new ArrayList<>(), 0, target, res);
        return res;
    }

    public void  dfs(int[] candidates, List<Integer> path, int index, int target, List<List<Integer>> res){
        if (target == 0 && !(res.contains(path))){
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i< candidates.length;i++){
            if (candidates[i] > target){
                break;
            }
            path.add(candidates[i]);
            dfs(candidates, path, i, target-candidates[i], res);
            path.remove(path.size() - 1);
        }
    }
}

public class Main {

    public static void main(String[] args) {
        Solution sol = new Solution();
        int [] nums = new int[]{2,3,5};
        List<List<Integer>> res = sol.combinationSum(nums, 8);
        System.out.print(res);
    }
}

40. 组合总和 II

题目描述

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

• 说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。

• 示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]

• 示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]

解题思路

和39差不多，加判断条件防止res中出现重复项，调用时为i+1，防止重复的数字。

class Solution(object):
    def combinationSum2(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        if len(candidates) == 0:
            return []
        res = []
        candidates.sort()
        self.dfs(candidates, target, 0, [], res)
        return res
    
    def dfs(self, candidates, residue, index, templist, res):
        if residue == 0 and templist not in res:
            res.append(templist)
            return
        for i in range(index, len(candidates)):
            if candidates[i] > residue:
                return
            self.dfs(candidates, residue-candidates[i], i+1, templist+[candidates[i]], res)

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if (candidates.length==0)
            return res;
        Arrays.sort(candidates);
        dfs(candidates, new ArrayList<>(), 0, target, res);
        return res;
    }

    public void  dfs(int[] candidates, List<Integer> path, int index, int target, List<List<Integer>> res){
        if (target == 0 && !(res.contains(path))){
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i< candidates.length;i++){
            if (candidates[i] > target){
                break;
            }
            path.add(candidates[i]);
            dfs(candidates, path, i+1, target-candidates[i], res);
            path.remove(path.size() - 1);
        }
    }
}

public class Main {

    public static void main(String[] args) {
        Solution sol = new Solution();
        int [] nums = new int[]{2,3,5};
        List<List<Integer>> res = sol.combinationSum(nums, 8);
        System.out.print(res);
    }
}

46. 全排列

题目描述

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

解题思路

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        res = []
        visited = [False] * len(nums)
        self.dfs(nums, [], visited, res)
        return res
    
    def dfs(self, nums, temp, visited, res):
        if len(temp) == len(nums):
            res.append(temp)
            return
        for i in range(len(nums)):
            if not visited[i]:
                visited[i] = True
                self.dfs(nums, temp+[nums[i]], visited, res)
                visited[i] = False

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        res = []
        self.dfs(nums, [], res)
        return res
    def dfs(self, nums, path, res):
        if not nums:
            res.append(path)
        for i in range(len(nums)):
            self.dfs(nums[:i]+nums[i+1:], path+[nums[i]], res)

import java.util.ArrayList;
import java.util.List;

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        dfs(nums, new ArrayList<>(), res);
        return res;
    }

    public void dfs(int[] nums, List<Integer> path, List<List<Integer>> res){
        if (path.size() == nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i<nums.length; i++){
            if (!(path.contains(nums[i]))){
                path.add(nums[i]);
                dfs(nums, path, res);
                path.remove(path.size()-1);
            }
        }
    }
}

public class Main {

    public static void main(String[] args) {
        Solution sol = new Solution();
        List<List<Integer>> res = sol.permute(new int []{1,2,3});
//        System.out.print();
    }
}

47. 全排列 II

题目描述

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

解题思路

class Solution(object):
    def permuteUnique(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        res = []
        visited = [False] * len(nums)
        self.dfs(nums, [], visited, res)
        return res
    def dfs(self, nums, temp, visited, res):
        if len(nums) == len(temp) and temp not in res:
            res.append(temp)
            return
        for i in range(len(nums)):
            if not visited[i]:
                visited[i] = True
                self.dfs(nums, temp+[nums[i]], visited, res)
                visited[i] = False

class Solution(object):
    def permuteUnique(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        res = []
        self.dfs(nums, [], res)
        return res
    def dfs(self, nums, temp, res):
        if not nums and temp not in res:
            res.append(temp)
        for i in range(len(nums)):
            self.dfs(nums[:i]+nums[i+1:], temp+[nums[i]], res)

51. N皇后

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

解题思路

N皇后定义：在n×n格的国际象棋上摆放n个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

回溯算法。
建立一个nxn的全是点的数组，从第0行开始遍历。
判断当前行是否已经超过矩阵范围，如果是，说明找到一种解法，加到res中。
否则，遍历当前行的所有列的位置，对于每一个位置，判断当前位置是否会产生冲突（isValid，判断两条对角线和一个垂直线），若当前行找到一个没有冲突的位置，则对下一行进行递归查找。

import copy
class Solution(object):
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        res = []
        queens = [['.'] * n for _ in range(n)]
        self.helper(0, queens, res)
        for queens in res:
            for i in range(len(queens)):
                queens[i] = ''.join(queens[i])
        return res

    def helper(self, curRow, queens, res):
        if curRow == len(queens):
            res.append(copy.deepcopy(queens))
            return
        for i in range(len(queens)):
            if self.isValid(queens, curRow, i):
                queens[curRow][i] = 'Q'
                self.helper(curRow + 1, queens, res)
                queens[curRow][i] = '.'

    def isValid(self, queens, row, col):
        for i in range(row):
            if queens[i][col] == 'Q':
                return False
        i, j = row - 1, col - 1
        while i >= 0 and j >= 0:
            if queens[i][j] == 'Q':
                return False
            i, j = i - 1, j - 1
        i, j = row - 1, col + 1
        while i >= 0 and j < len(queens):
            if queens[i][j] == 'Q':
                return False
            i, j = i - 1, j + 1
        return True

52. N皇后 II

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

解题思路

class Solution(object):
    def totalNQueens(self, n):
        """
        :type n: int
        :rtype: int
        """
        
        self.res = 0
        queens = [['.']*n for _ in range(n)]
        self.helper(0, queens)
        return self.res
    
    def helper(self, curRow, queens):
        if curRow == len(queens):
            self.res += 1
            return
        for i in range(len(queens)):
            if self.isValid(queens, curRow, i):
                queens[curRow][i] = 'Q'
                self.helper(curRow+1, queens)
                queens[curRow][i] = '.'
    
    def isValid(self, queens, row, col):
        for i in range(row):
            if queens[i][col] == 'Q':
                return False
        i, j = row-1, col-1
        while i >= 0 and j >= 0:
            if queens[i][j] == 'Q':
                return False
            i, j = i-1, j-1
        i, j = row-1, col+1
        while i >= 0 and j < len(queens):
            if queens[i][j] == 'Q':
                return False
            i, j = i-1, j+1
        return True

60. 第k个排列

题目描述

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

1. “123”
2. “132”
3. “213”
4. “231”
5. “312”
6. “321”

给定 n 和 k，返回第 k 个排列。

说明：

给定 n 的范围是 [1, 9]。
给定 k 的范围是[1, n!]。

示例 1:

输入: n = 3, k = 3
输出: “213”

示例 2:

输入: n = 4, k = 9
输出: “2314”

解题思路

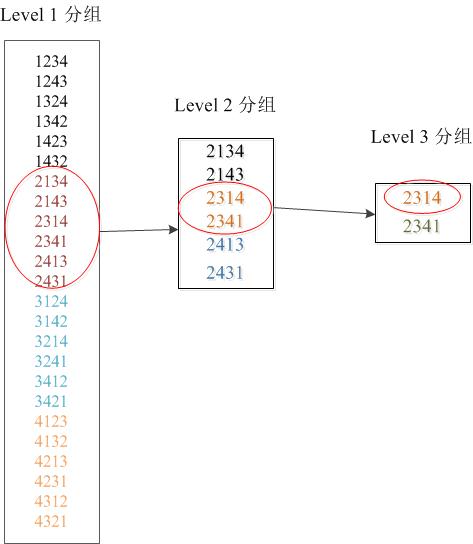
所有元素共有 n! 种排列。根据下图对’1234’的全排列，按照第一个字符可以分为4组，按照第二个字符可以分为3组，按照第三个字符可以分为2组，所以一共有4x3x2种排列方式。

要得到第九个排列’2314’，转换为数组下标也就是8，在level 1 中下标为1，level 2 中下标为1，level 3 中下标为0。具体过程为：

• 最高位可以取{1,2,3,4}，并且每个数在最高位出现3!=6次，第9个排序的最高位下标为：8//3!=1，也就是2；
• 次位可以取{1,3,4}，并且每个数在次位出现2!=2次，第9个排序的最高位下标为：(8%6)//2!=1，也就是3;
• 第三位可以取{1,4},并且每个数在第三位出现1次，第9个排列的第三位取值下标为：(8%6%2)//1=0，也就是1；
• 最后一位只有一个数字4。

用ki表示在数组中的取值下标，n表示集合中数字个数：

• k = k-1，此步是关键
• k1 = k//(n-1)!
• k = k%(n-1)!
• k2 = k//(n-2)!
• k = k%(n-2)!
• …
• kn-1 = k//1

参考文章

class Solution(object):
    def getPermutation(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: str
        """
        if n <= 0:
            return ''
        fact = [1]*n
        for i in range(1,n):
            fact[i] = fact[i-1]*i
        if k > fact[-1]*n:
            return ''
        k = k-1
        res = ''
        num = [str(i) for i in range(1,n+1)]
        for i in range(n, 0, -1):
            index = k // fact[i-1]
            res += num[index]
            k = k % fact[i-1]
            num.pop(index)
        return res

77. 组合

题目描述

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

解题思路

回溯法，我们抽取第一个字符，然后从后面n-1个字符中抽取k-1个；抽取第二个字符，再从后面的n-2个字符抽出k-1.

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        if n <= 0 or k <= 0:
            return []
        
        res = []
        self.dfs(range(1, n+1), k, [], res)
        return res
    
    def dfs(self, nums, k, path, res):
        if k > len(nums):
            return
        if k == 0:
            res.append(path)
            return 
        for i in range(len(nums)):
            self.dfs(nums[i+1:], k-1, path+[nums[i]], res)

78. 子集

题目描述

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

解题思路

class Solution(object):
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return [[]]
        res = []
        self.dfs(nums, 0, res, [])
        return res
    
    def dfs(self, nums, index, res, path):
        res.append(path)
        for i in range(index, len(nums)):
            self.dfs(nums, i+1, res, path+[nums[i]])

79. 单词搜索

题目描述

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

解题思路

Leetcode65题

class Solution(object):
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """
        
        if len(board) == 0:
            return False
        
        if len(word) == 0:
            return True
        
        visited = [[False]*len(board[0]) for i in range(len(board))]
        
        for i in range(len(board)):
            for j in range(len(board[0])):
                if self.helper(board, word, i, j, 0, visited):
                    return True
        return False
    
    def helper(self, board, word, i, j, pathlength, visited):
        if pathlength == len(word):
            return True
        curHaspath = False
        if 0<=i<len(board) and 0<=j<len(board[0]) and board[i][j] == word[pathlength] and not visited[i][j]:
            visited[i][j] = True
            pathlength += 1
            curHaspath = self.helper(board,word,i+1,j,pathlength,visited) or self.helper(board,word,i-1,j,pathlength,visited) or self.helper(board,word,i,j+1,pathlength,visited) or self.helper(board,word,i,j-1,pathlength,visited)
            if not curHaspath:
                visited[i][j] = False
                pathlength -= 1
        return curHaspath

89. 格雷编码

题目描述

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

示例 1:

输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

示例 2:

输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。
     给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。
     因此，当 n = 0 时，其格雷编码序列为 [0]。

解题思路

格雷码的生成过程：res[i] = i ^ (i//2)。
如n = 3：

• res[0] = 0 = 000
• res[1] = 1^(1//2) = 001^000 = 001
• res[2] = 2^(2//2) = 010^001 = 011
• res[3] = 3^(3//2) = 011^001 = 010
• res[4] = 4^(4//2) = 100^010 = 110
• res[5] = 5^(5//2) = 101^010 = 111
• res[6] = 6^(6//2) = 110^011 = 101
• res[7] = 7^(7//2) = 111^011 = 100

class Solution(object):
    def grayCode(self, n):
        """
        :type n: int
        :rtype: List[int]
        """
        if n < 0:
            return []
        num = 1
        for i in range(n):
            num *= 2
        res = [0]*num
        while i < num:
            res[i] = i ^ (i//2)
            i += 1
        return res

class Solution(object):
    def grayCode(self, n):
        """
        :type n: int
        :rtype: List[int]
        """
        if n < 0:
            return []
        
        res = [0]*(2**n)
        
        for i in range(len(res)):
            res[i] = i^(i//2)
            
        
        return res

90. 子集 II

题目描述

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

解题思路

class Solution(object):
    def subsetsWithDup(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if len(nums) == 0:
            return []
        
        nums.sort()
        res = []
        self.dfs(nums, 0, [], res)
        return res
    
    def dfs(self, nums, index, path, res):
        if path not in res:
            res.append(path)
        for i in range(index, len(nums)):
            if i > index and nums[i] == nums[i-1]:
                continue
            self.dfs(nums, i+1, path+[nums[i]], res)

93. 复原IP地址

题目描述

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

示例:

输入: “25525511135”
输出: [“255.255.11.135”, “255.255.111.35”]

解题思路

IP地址由四部分组成，每一部分的数字为0~255，使用回溯算法验证每一部分的数字大小,一部分数字做多为3位（range(1,4))，在使用完字符串中所有字符且当前IP地址为四部分时添加到结果中。
每次dfs的时候都去检查一下所有的字符串的长度是不是能满足在最多4个3位数字组成。

class Solution(object):
    def restoreIpAddresses(self, s):
        """
        :type s: str
        :rtype: List[str]
        """
        if not s or len(s) < 4 or len(s) > 12:
            return []
        res = []
        self.dfs(s, [], res)
        return res
    
    def dfs(self, s, temp, res):
        if not s and len(temp) == 4:
            res.append('.'.join(temp))
            return
        if len(temp) >= 4 or len(s) > (4-len(temp))*3:
            return 
        for i in range(1, 4):
            if i > len(s):
                continue
            number = int(s[:i])
            if str(number) == s[:i] and number <= 255:
                self.dfs(s[i:], temp + [s[:i]], res)

131. 分割回文串

题目描述

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例:

输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

解题思路

在每次回溯之前判断当前字符串是否为回文串。

class Solution(object):
    def partition(self, s):
        """
        :type s: str
        :rtype: List[List[str]]
        """
        if not s:
            return []
        res = []
        self.dfs(s, [], res)
        return res
    
    def dfs(self, s, temp, res):
        if not s and temp:
            res.append(temp)
            return
        for i in range(1, len(s)+1):
            if self.isPalindrome(s[:i]):
                self.dfs(s[i:], temp+[s[:i]], res)
    
    def isPalindrome(self, s):
        # left, right = 0, len(s)-1
        # while left <= right:
        #     if s[left] != s[right]:
        #         return False
        #     left += 1
        #     right -= 1
        # return True
        return s == s[::-1]

216. 组合总和 III

题目描述

找出所有相加之和为 n的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1:

**输入:*****k*** = 3, ***n*** = 7
**输出:** [[1,2,4]]

示例 2:

**输入:*****k*** = 3, ***n*** = 9
**输出:** [[1,2,6], [1,3,5], [2,3,4]]

解题思路

class Solution(object):
    def combinationSum3(self, k, n):
        """
        :type k: int
        :type n: int
        :rtype: List[List[int]]
        """
        
        if k == 0 or n == 0:
            return []
        
        res = []
        self.help(k, 1, n, [], res)
        return res
    
    def help(self, k, index, n, path, res):
        if k == 0:
            if n == 0:
                res.append(path)
            return
        for i in range(index, 10):
            if n - i < 0:
                break
            self.help(k-1, i+1, n-i, path + [i], res)