本系列为数据结构学习笔记(待汇总)。
红黑树定义
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在$O(logn)$时间内做查找,插入和删除,这里的$n$是树中元素的数目。
红黑树性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。除二叉查找树强制的一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 性质1:节点是红色或黑色
- 性质2:根节点是黑色
- 性质3:所有叶子节点都是黑色(叶子是NIL节点)
- 性质4:每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 性质5.:从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
注意:
- 性质3中的叶子节点,是只为空(NIL或null)的节点。
- 性质5确保从根到叶子的最长的可能路径不多于最短的可能路径的两倍长,因而,红黑树是相对是接近平衡的二叉树。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
- 要知道为什么这些性质确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
红黑树示例: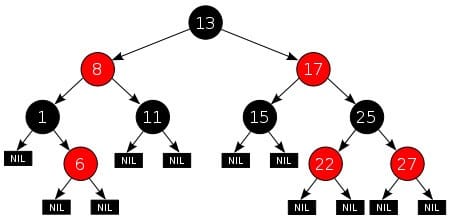
红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(logn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++的STL中的Set、Map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
红黑树基本操作
左旋
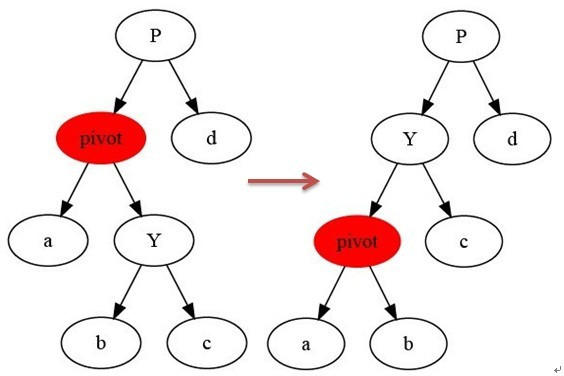
如上图所示,当在某个结点pivot上,做左旋操作时,我们假设它的右孩子Y不是NULL,pivot可以为任何不是NULL的左子结点。左旋以pivot到Y之间的链为“支轴”进行,它使Y成为该子树的新根,而Y的左孩子b则成为pivot的右孩子。
右旋
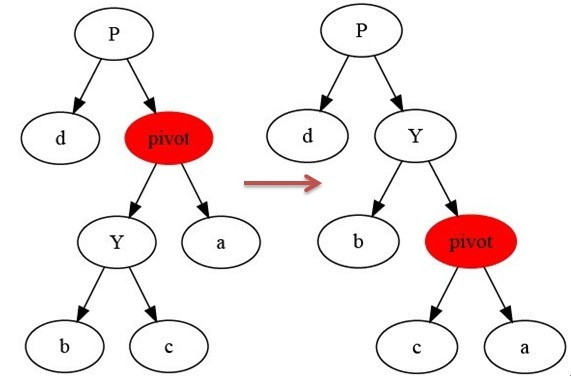
如上图所示,当在某个结点pivot上,做右旋操作时,我们假设它的左孩子Y不是NULL,pivot可以为任何不是NULL的右子结点。右旋以Y到pivot之间的链为“支轴”进行,它使Y成为该子树的新根,而Y的右孩子b则成为pivot的左孩子。

