本系列为数据结构学习笔记(待汇总)。
布隆过滤器
背景
虽然位图可以节省空间,但是数据量大的时候需要的内存还是比较大的。布隆过滤器就是为了解决这个问题,对位图数据结构的一种改进。
举例:考虑数据个数是1千万,数字范围是1到10亿,使用位图需要10亿个二进制位,而布隆过滤器的做法是,使用一个1亿个二进制大小的位图,然后通过哈希函数,对数字进行处理,让它落在这1到1亿范围内。比如我们把哈希函数设计成 $f(x)=x%n$。其中,x表示数字,n表示位图的大小(1亿),也就是,对数字跟位图的大小进行取模求余。
这时哈希函数会存在冲突的问题啊,一亿零一和1两个数字,经过你刚刚那个取模求余的哈希函数处理之后,最后的结果都是1。这样我就无法区分,位图存储的是1还是一亿零一了。如何降低冲突的概率?用K个哈希函数!!
布隆过滤器定义
布隆过滤器是一种空间效率很高的随机数据结构,它的原理是当一个元素被加入集合时,通过K个Hash函数将这个元素映射成一个位阵列(Bit array)中的K个点,将它们置为1。检索时,我们只要看看这些点是不是都是1就大约知道集合中有没有它了:如果这些点有任何一个点为0,则被检索元素一定不在;如果都是1,则被检索元素很可能在。这就是布隆过滤器的基本思想。
但布隆过滤器的这种高效是有代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。因此,Bloom filter不适合那些“零错误”的应用场合。而在能容忍低错误率的场景下,布隆过滤器通过极少的错误换取了存储空间的极大节省。
布隆过滤器的误判有一个特点,那就是,它只会对存在的情况有误判。如果某个数字经过布隆过滤器判断不存在,那说明这个数字真的不存在,不会发生误判;如果某个数字经过布隆过滤器判断存在,这个时候才会有可能误判,有可能并不存在。不过,只要我们调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例,那就可以将这种误判的概率降到非常低。
集合表示和元素查询
具体来看Bloom Filter是如何用位数组表示集合的。初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0。
为了表达$ \mathrm{S}=\left\{\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}\right\} $这样一个$n$个元素的集合,Bloom Filter使用$k$个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到$\{1,…,m\}$的范围中。对任意一个元素$x$,第$i$个哈希函数映射的位置$h_i(x)$就会被置为1($1≤i≤k$)。注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位,即第二个“1“处)。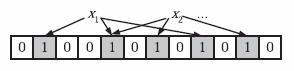
在判断y是否属于这个集合时,我们对y应用k次哈希函数,如果所有$h_i(y)$的位置都是1(1≤i≤k),那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中$y_1$就不是集合中的元素(因为$y_1$有一处指向了“0”位)。$y_2$或者属于这个集合,或者刚好是一个false positive。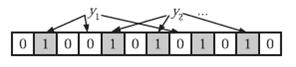
位数组大小
对于给定的p(误判率)和将要加入集合的元素个数n,位数组大小m由如下公式定义:
最优的哈希函数个数
对于给定的位数组大小m和将要加入集合的元素个数n,使得误判率最小的哈希函数个数k通过如下公式定义:
误判率估计
对于给定的位数组大小m,将要加入集合的元素个数n,及哈希函数个数k,误判率可以重新计算为:
应用
在计算机科学中,我们常常会碰到时间换空间或者空间换时间的情况,即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素:错误率。在使用Bloom Filter判断一个元素是否属于某个集合时,会有一定的错误率。也就是说,有可能把不属于这个集合的元素误认为属于这个集合(False Positive),但不会把属于这个集合的元素误认为不属于这个集合(False Negative)。在增加了错误率这个因素之后,Bloom Filter通过允许少量的错误来节省大量的存储空间。
Bloom Filter就被广泛用于拼写检查和数据库系统中。 也可以用来实现数据字典,进行数据的判重,或者集合求交集 。
参考文献:
https://blog.csdn.net/v_july_v/article/details/6685894
https://blog.csdn.net/jiaomeng/article/details/1495500
https://blog.csdn.net/tick_tock97/article/details/78688159

